Démarche statistique
remi.mahmoud@institut-agro.fr
https://demarche-stat-lesson.netlify.app
Introduction
Objectifs
- Aborder les problèmes courants en analyse de données
- Argumenter le choix de procédures d’analyses
- Mettre en oeuvre une démarche d’analyse de données avec

- Interpréter & restituer les résultats d’une analyse
On attend:
Attention
Réflexion
Participation
Evaluation:
2 CC (50%) + 1 projet (50%)
Quelques définitions (Wiki)
LA statistique: discipline qui étudie les phénomènes à travers la collecte de données, leur traitement, leur analyse, l’interprétation et la présentation des résultats […]. Domaine des mathématiques + boîte à outils. Fait partie de la science des données
LES statistiques: type d’information obtenu en soumettant les valeurs à des opérations mathématiques.
L’analyse des données: Famille de méthodes statistiques dont les principales caractéristiques sont d’être multidimensionnelles et descriptives.
: en anglais, data analysis ⇔ Statistique
En résumé
La statistique s’intéresse à des jeux de données de taille raisonnable, fréquents dans vos domaines.
Les statistiques sont (utilisées) partout
- En cela elles sont un outil politique, traduisant une certaine vision du monde et à manipuler avec précaution.
Coeur de la statistique
- Avoir les bonnes données:
- observations d’un phénomène
- sont-elles représentatives ?
Ex. où renforcer l’avion ?
Les résumer, les visualiser
Se poser des questions:
- Ex. pollution aux algues vertes: quelle variable utiliser ? Surface ? Masse ? Où/Quand/Comment faire des recueils ?
- Cause / Conséquence (variété de blé / Rendement ; utilisation de phyto / diversité entomologique ; complexité du paysage)
- Variables explicatives vs variable(s) réponse(s)
- Tous les effets ont-ils été pris en compte ?
Ex. paradoxe de Simpson (Vidéo complète sur le sujet de Science Etonnante)
Outil: R (moteur) / Rstudio (carrosserie)
- Gratuit/libre/multi-plateforme
- Nombreux (+++) domaines d’applications (ex. ce cours a été réalisé sous R)
- BEAUCOUP d’aide dispo
Installation:
- Télécharger et installer le moteur
 → https://cran.r-project.org/
→ https://cran.r-project.org/
- Télécharger et installer la carrosserie

On peut aussi dessiner avec R (mais c’est une autre histoire)


Quelques définitions (1/2)
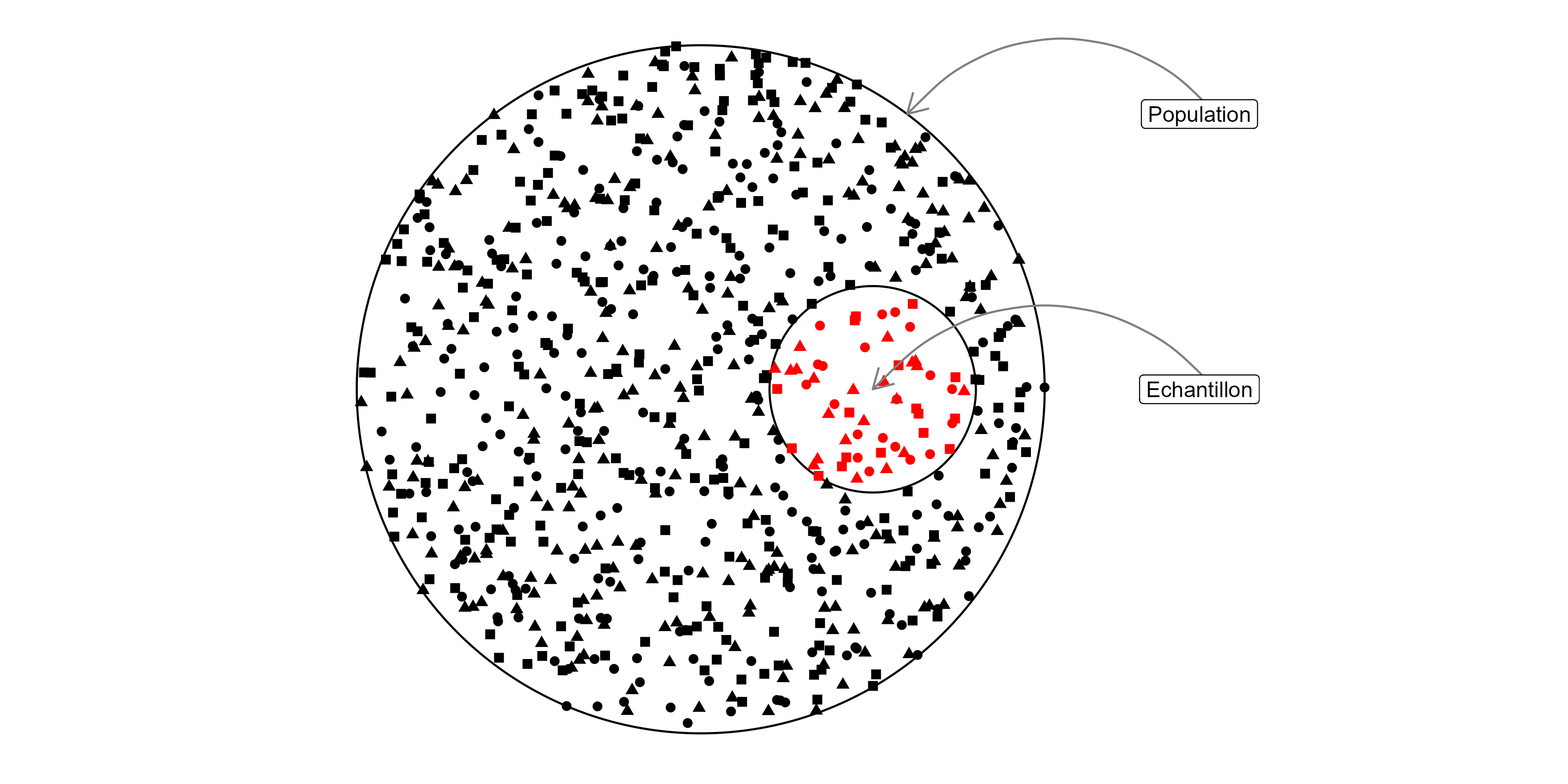
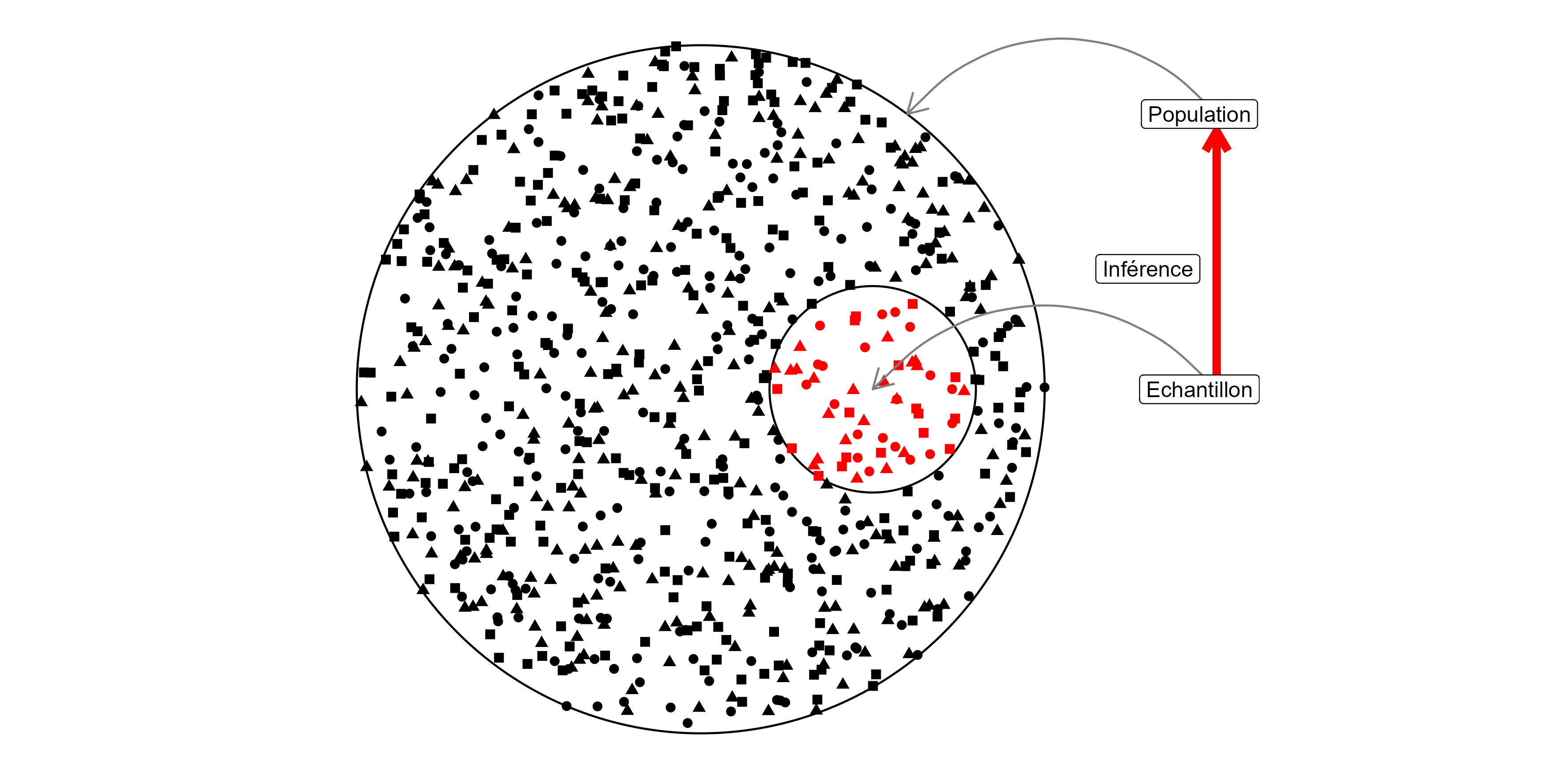
Population: ensemble d’entités objet de l’investigation statistique
Individu: élément de la population d’étude
Echantillon: ensemble des individus pour lesquels des valeurs ont été observées pour les variables de l’étude
Variable: descripteur ou caractère des individus de la population d’étude
Inférence: décider pour une population à partir des données observées de l’échantillon

Quelques définitions (2/2)
Nature des variables:
- Qualitatives : les valeurs prises sont des modalités
- nominale : pas de structure d’ordre
- ordinale : modalités ordonnées
- quantitative: les valeurs prises sont numériques
- discrete
- continue $
Décrire les données à l’aide d’indicateurs
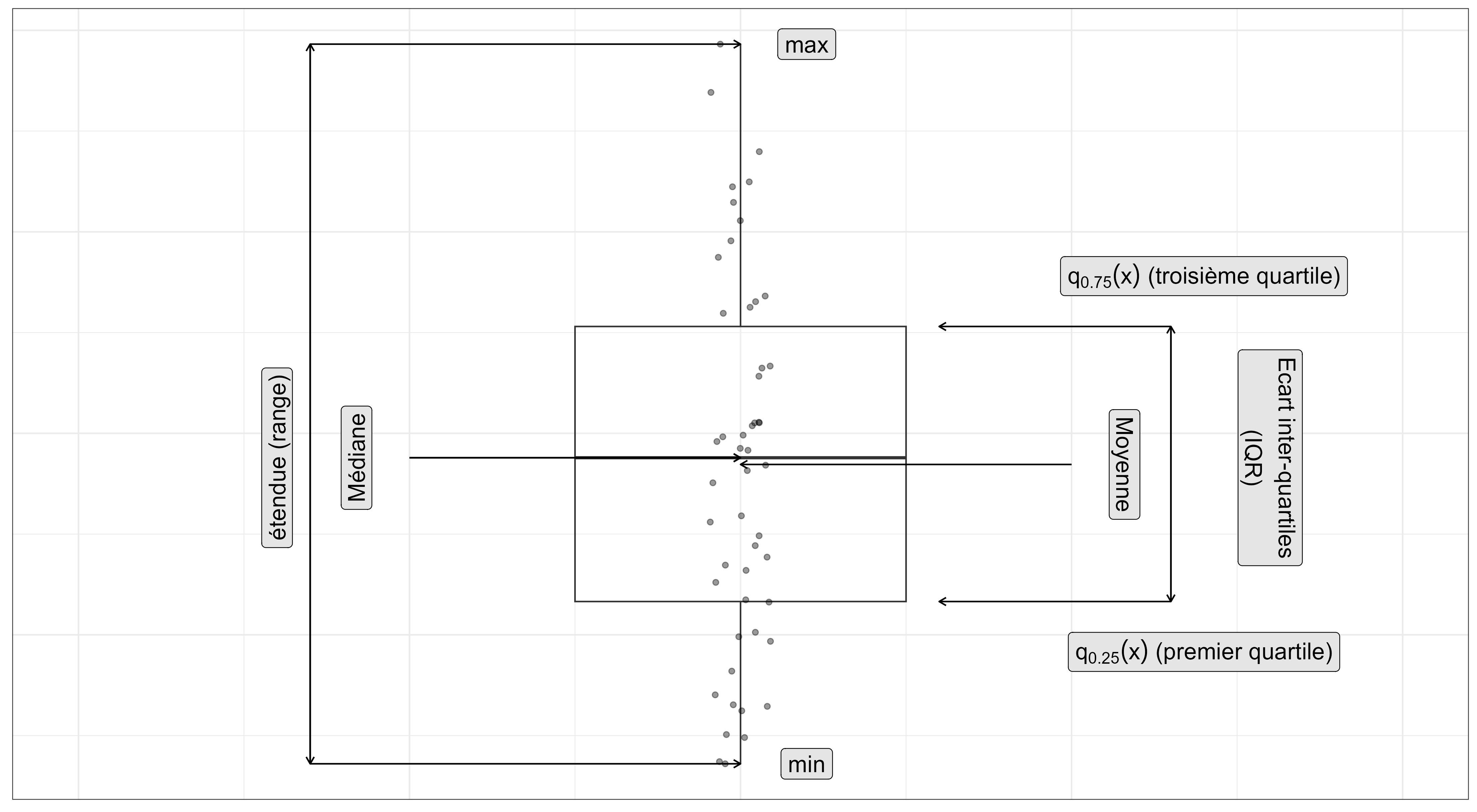
Soit x1,x2,...,xn une série de n valeurs d’une variable X. On peut les décrire en utilisant des indicateurs de position et de dispersion (que vous connaissez probablement)
- moyenne: ˉx=1n∑xi=x1+x2+...+xnn
- médiane: q0.5(x)= valeur telle que 50% des xi ont une valeur inférieure et 50% une valeur supérieure
- 1er quartile: q0.25(x)= valeur telle que 25% des xi ont une valeur inférieure et 75% une valeur supérieure
- 3ème quartile: q0.75(x)= valeur telle que 75% des xi ont une valeur inférieure et 25% une valeur supérieure
- quantile α: qα(x)= valeur telle que 100×α % des xi ont une valeur inférieure et 100−100×α% une valeur supérieure
- variance: s2(x)=ˆσ2(x)=1n−1∑(xi−ˉx)2
- écart-type: s(x)=√s2(x)
Un jeu de données comme fil conducteur
L’association Air Breizh surveille la qualité de l’air et mesure la concentration de polluants comme l’ozone (O3, en μg.m−3) ainsi que les conditions météorologiques comme la température, la nébulosité, le vent, etc. Durant l’été 2001, 112 données ont été relevées à Rennes.
maxO3 T9 T12 T15 Ne9 Ne12 Ne15 Vx9 Vx12 Vx15 maxO3v vent pluie
87 15.6 18.5 18.4 4 4 8 0.6946 -1.7101 -0.6946 84 Nord Sec
82 17.0 18.4 17.7 5 5 7 -4.3301 -4.0000 -3.0000 87 Nord Sec
92 15.3 17.6 19.5 2 5 4 2.9544 1.8794 0.5209 82 Est Sec
114 16.2 19.7 22.5 1 1 0 0.9848 0.3473 -0.1736 92 Nord Sec
94 17.4 20.5 20.4 8 8 7 -0.5000 -2.9544 -4.3301 114 Ouest Sec
80 17.7 19.8 18.3 6 6 7 -5.6382 -5.0000 -6.0000 94 Ouest PluieUne question:
- Peut-on prévoir la concentration en ozone du lendemain pour avertir la population en cas de pic de pollution ?
Visualisation
La visualisation: pourquoi ?
- Quels points communs entre ces 4 jeux de données ?
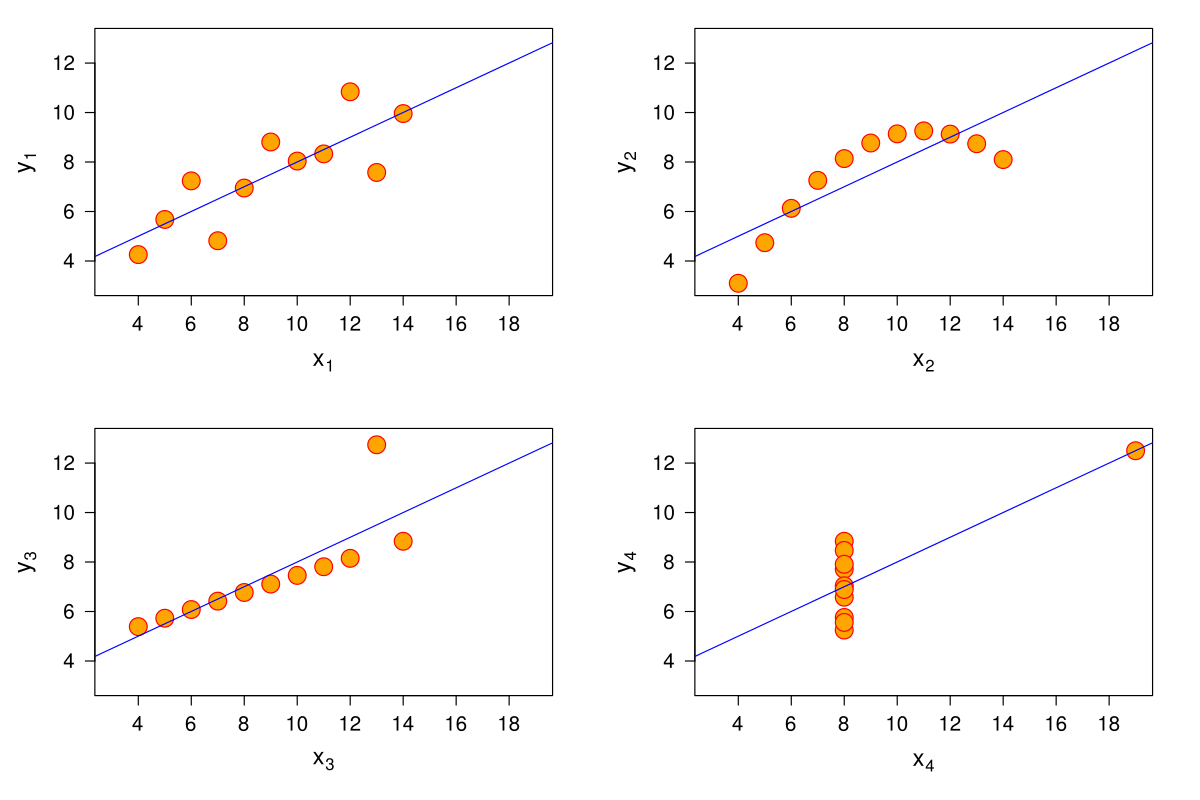
Visualisation: quels choix ?
- La visualisation dépend de:
La nature des données (nature des variables, nb d’individus)
La problématique: qu’est-ce que je veux montrer ?
le site data-to-viz.com permet de trouver de bonnes idées
- La visualisation permet de:
- comprendre / explorer / vérifier les données
- suggérer des analyses
- faire passer des idées
Les graphiques sont ce qu’on retient de nombreux rapports / analyses / articles scientifiques.
Sur  , le package
, le package ggplot2 permet de faire des visualisations allant du plus simple au plus compliqué.
GGplot - Quick tuto

GGplot - Exemple: distribution d’une variable quantitative

GGplot - Exemple: distribution d’une variable quantitative

GGplot - Exemple: distribution d’une variable quantitative
GGplot - Exemple: distribution d’une variable quantitative
GGplot - Exemple: distribution d’une variable quantitative
GGplot - Exemple: distribution d’une variable quantitative
Moche ? Pensez à theme_bw() (black & white)
Distribution d’une variable qualitative (1/2)
Le camembert c’est bon, mais seulement en fromage. SINON CA PUE TROP.
Quelle classe est la plus représentée ?
Distribution d’une variable qualitative (2/2)
Alternative: graphiques en barre
Code
Code
library(dplyr)
ozone %>%
summarise(prop_vent = n()/nrow(ozone), .by = vent) %>% # On résume le jeu de donnée par direction de vent, on calcule le nb de chaque catégorie sur la longueur totale du jeu de données
mutate(vent = reorder(vent, prop_vent)) %>% # trier le facteur pour ordonner les catégories
ggplot(aes(x = vent, y= prop_vent)) +
labs(y = "%") +
geom_col(alpha = .5)+ # 50% de transparence
scale_y_continuous(labels=scales::percent) +
geom_text(aes(label=scales::percent(prop_vent)), vjust = -1.5)+
theme_bw()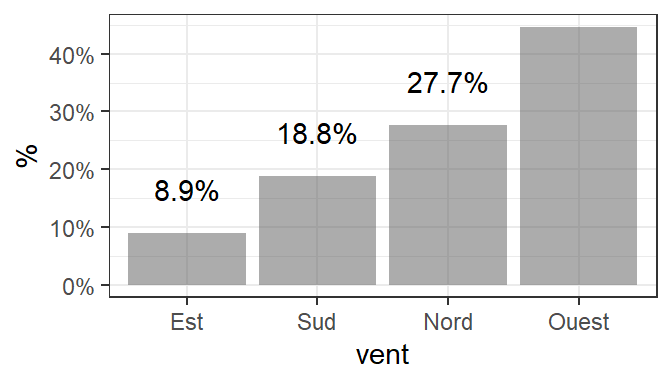
Effet d’une / deux variable(s) sur une variable quanti
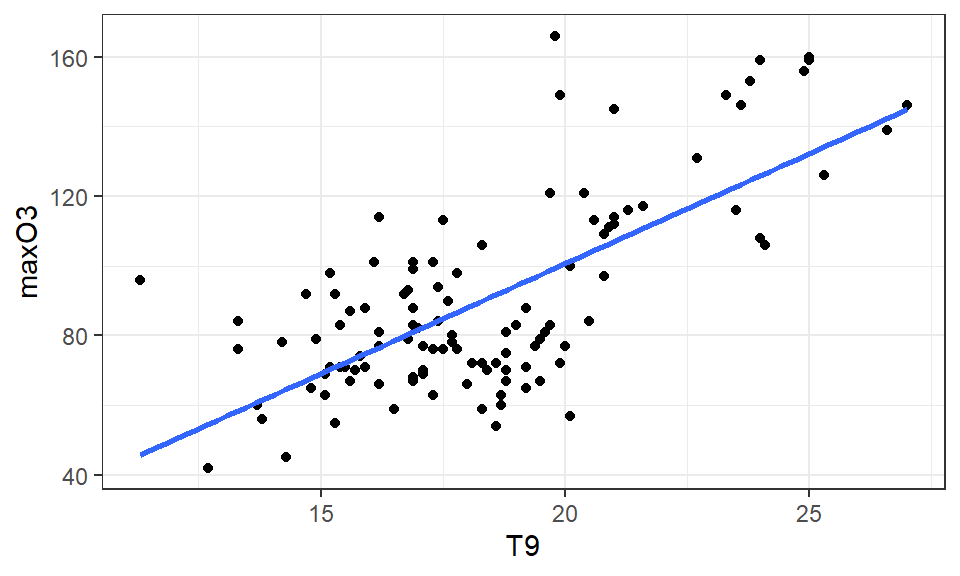
Effet d’une / deux variable(s) quali sur une variable quanti (1/2)
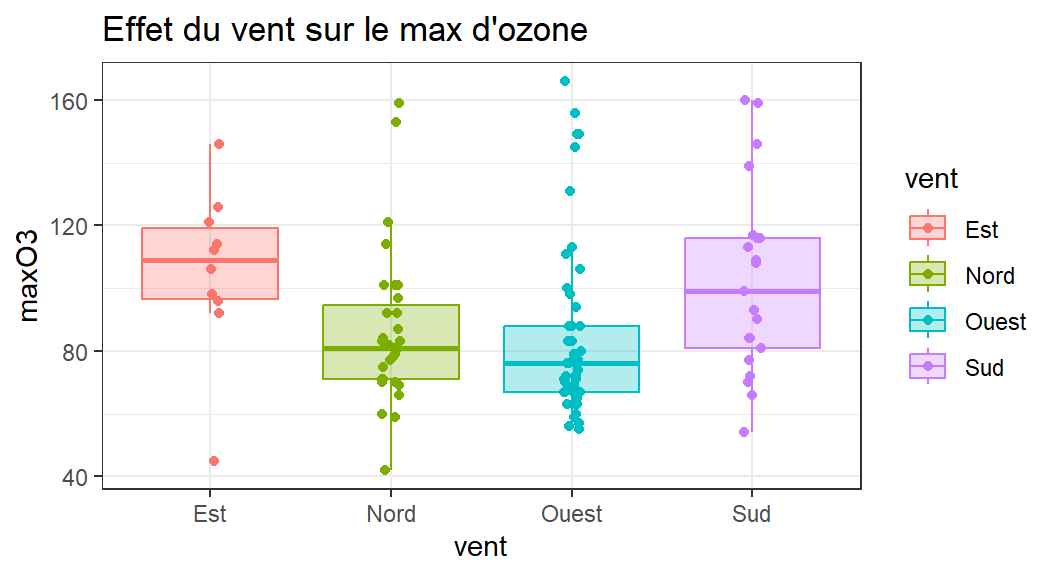
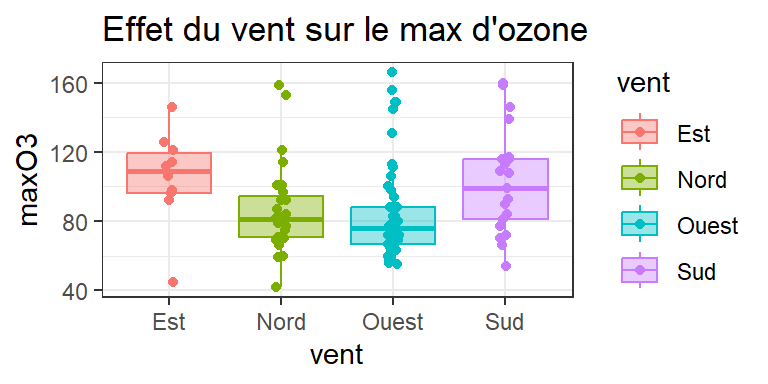
ggplot(ozone, aes(x = vent,
y= maxO3,
fill=vent,
col=vent)) + # dans aes: ce qui DEPEND du jeu de données
geom_boxplot(outlier.shape=NA,alpha=0.4) + # alpha : transparence
geom_point(position = position_jitter(width = 0.05, height= 0)) + # ajout
# points, avec perturbation horizontale pour faciliter visu
theme_bw() +
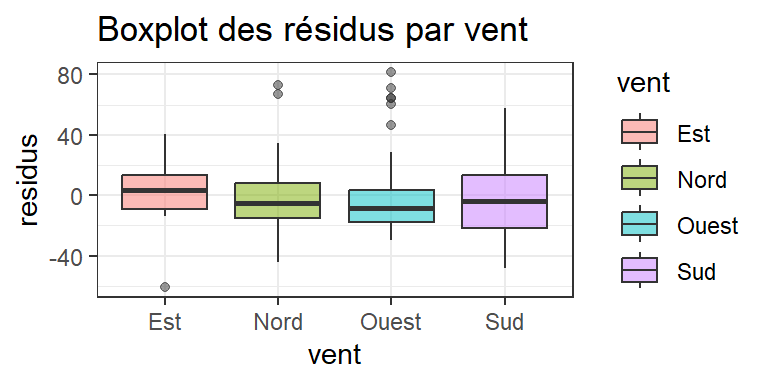
labs(title ="Effet du vent sur le max d'ozone")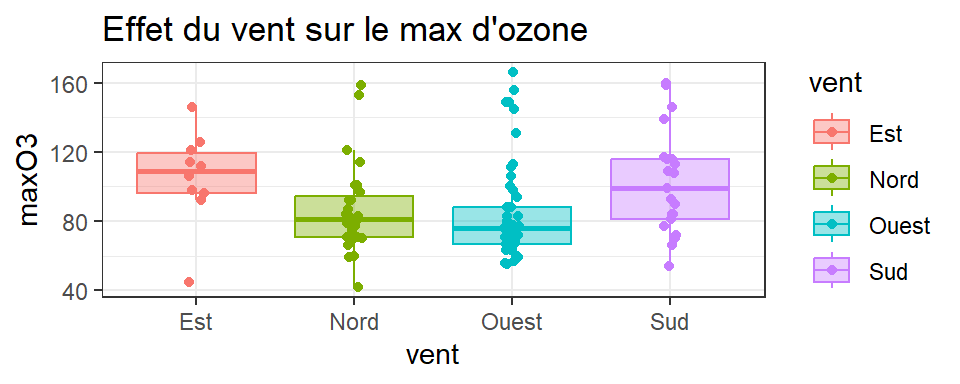
Effet de deux variable(s) quali sur une variable quanti (2/2)
Quid d’une interaction potentielle vent pluie ?
Code
library(dplyr)
ozone %>%
summarise(moy_O3 = mean(maxO3), .by = c(vent, pluie)) %>%
# MOYENNER LES VALEURS DE MAXO3 PAR VENT ET PLUIE
#ET PASSER LE RESULTAT DANS GGPLOT VIA %>%
ggplot(aes(x = vent, y= moy_O3, group = pluie, color =pluie)) +
geom_line() +
geom_point() +
theme_bw() +
labs(title ="Interaction pluie:vent sur le max03",
y = "Moyenne de maxO3", x = "Direction du vent")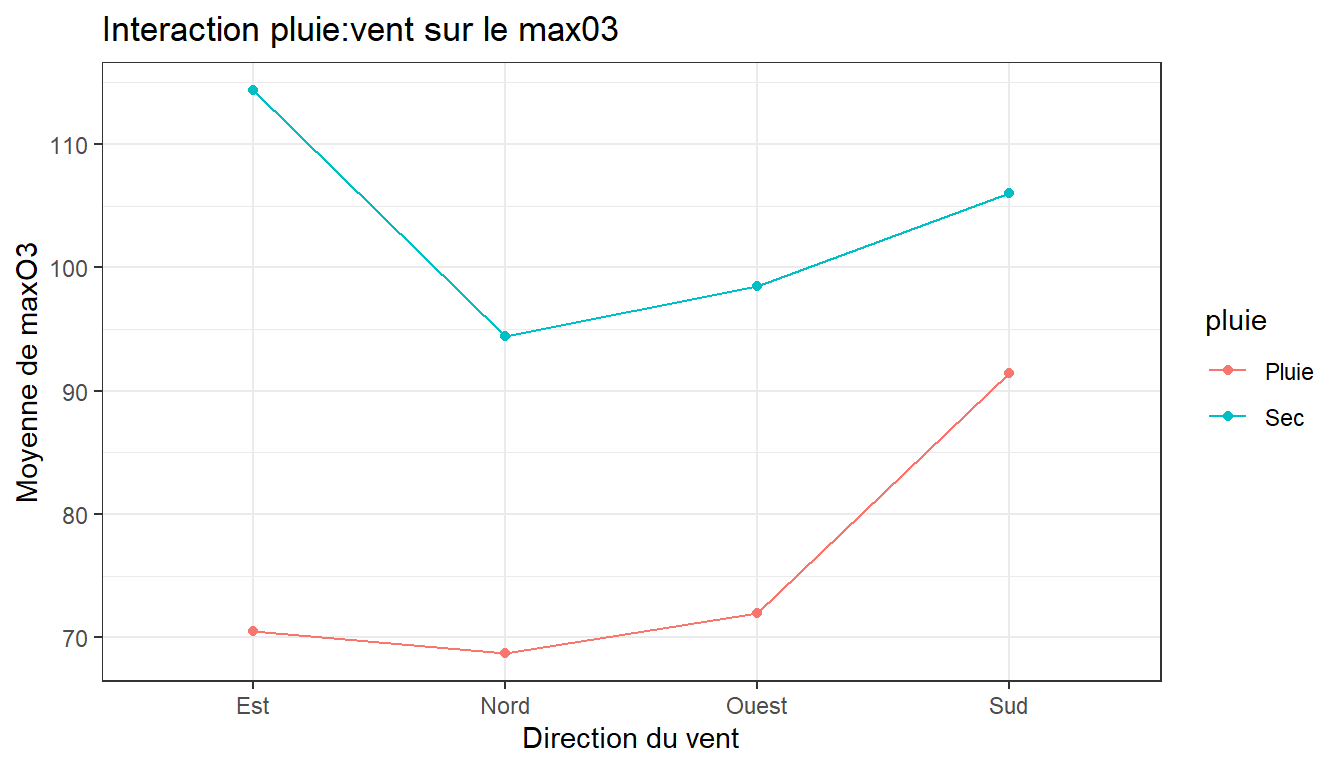
Des visualisations vers les tests statistiques
Les visus précédentes nous ont permis d’intuiter certaines tendances.
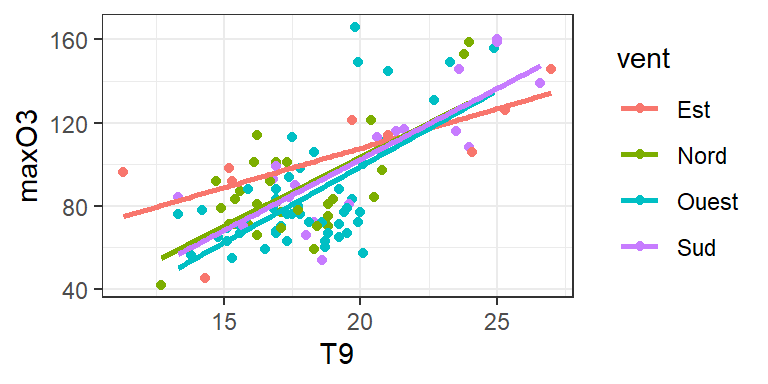
Peut-on les généraliser ? Rappel:

C’est toute la question des tests statistiques.
Principes et applications des tests statistiques
De la question aux tests
- On dispose de multiples variables, toutes présentant potentiellement un intérêt
[1] "maxO3" "T9" "T12" "T15" "Ne9" "Ne12" "Ne15" "Vx9"
[9] "Vx12" "Vx15" "maxO3v" "vent" "pluie" - Ici une variable particulière nous intéresse (c’est un choix ; guidé par la littérature scientifique / les politiques publiques etc. ): maxO3 (car étant clé pour la pollution de l’air). C’est la variable réponse
On peut se poser plusieurs questions:
- Effet du vent sur le max d’ozone ?
- Le temps sec/pluvieux influence-t-il le max d’ozone ? De la même manière selon les différentes directions du vent ?
Objectif : Généraliser (inférer) au-delà des données de l’échantillon
Problème : Comment gérer l’incertitude liée au fait qu’on a observé qu’une petite partie des données
Faisons d’abord un détour par la notion de distribution statistique et de loi de probabilité
Rappel sur la notion de distribution statistique / loi de probabilité
Définition :
Une distribution statistique décrit comment les valeurs d’une variable se répartissent dans un ensemble de données.Types de variables :
- Quantitatives : mesurables (ex : taille des plantes).
- Qualitatives : catégories (ex : variétés de cultures).
En théorie, une distribution peut s’approcher d’une loi de probabilité.
Un exemple classique de loi de probabilité que vous connaissez probablement : la loi normale.
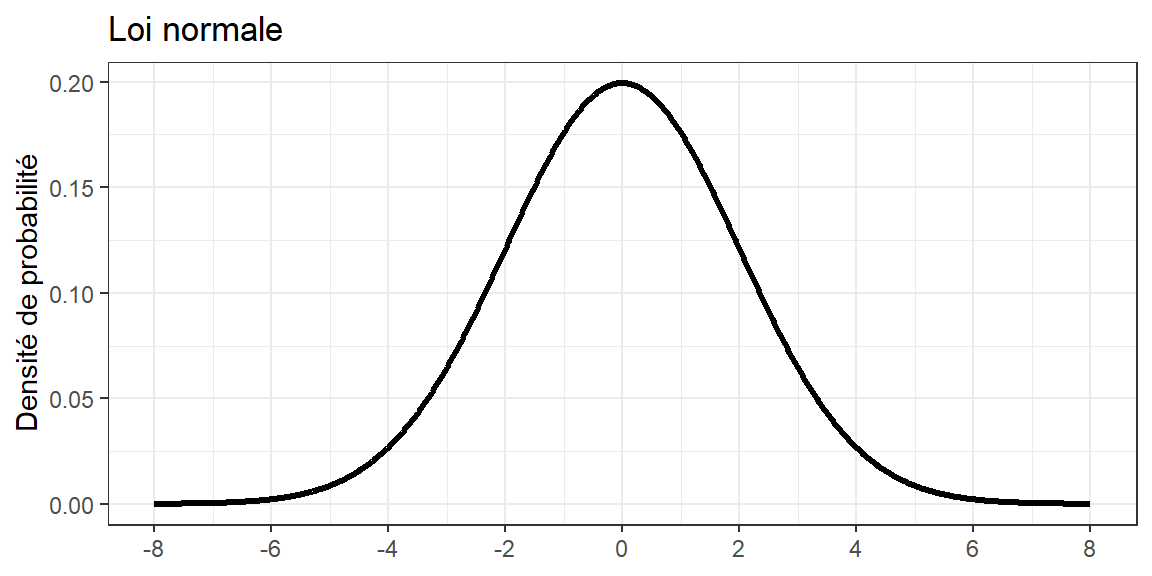
Interprétation probabiliste
- La probabilité qu’une variable aléatoire appartienne à un intervalle donné est proportionnelle à la surface sous la courbe de distribution pour cet intervalle.
Décrire une loi de probabilité
Il existe de beaucoup de lois de probabilités, qu’on peut décrire via différents paramètres.
Quelques paramètres descriptifs d’une loi
- Tendance centrale :
- Moyenne : la “valeur attendue”.
- Médiane : la valeur au milieu de la distribution.
- Mode : la valeur la plus fréquente.
- Dispersion :
- Variance / écart-type
- IQR / étendue
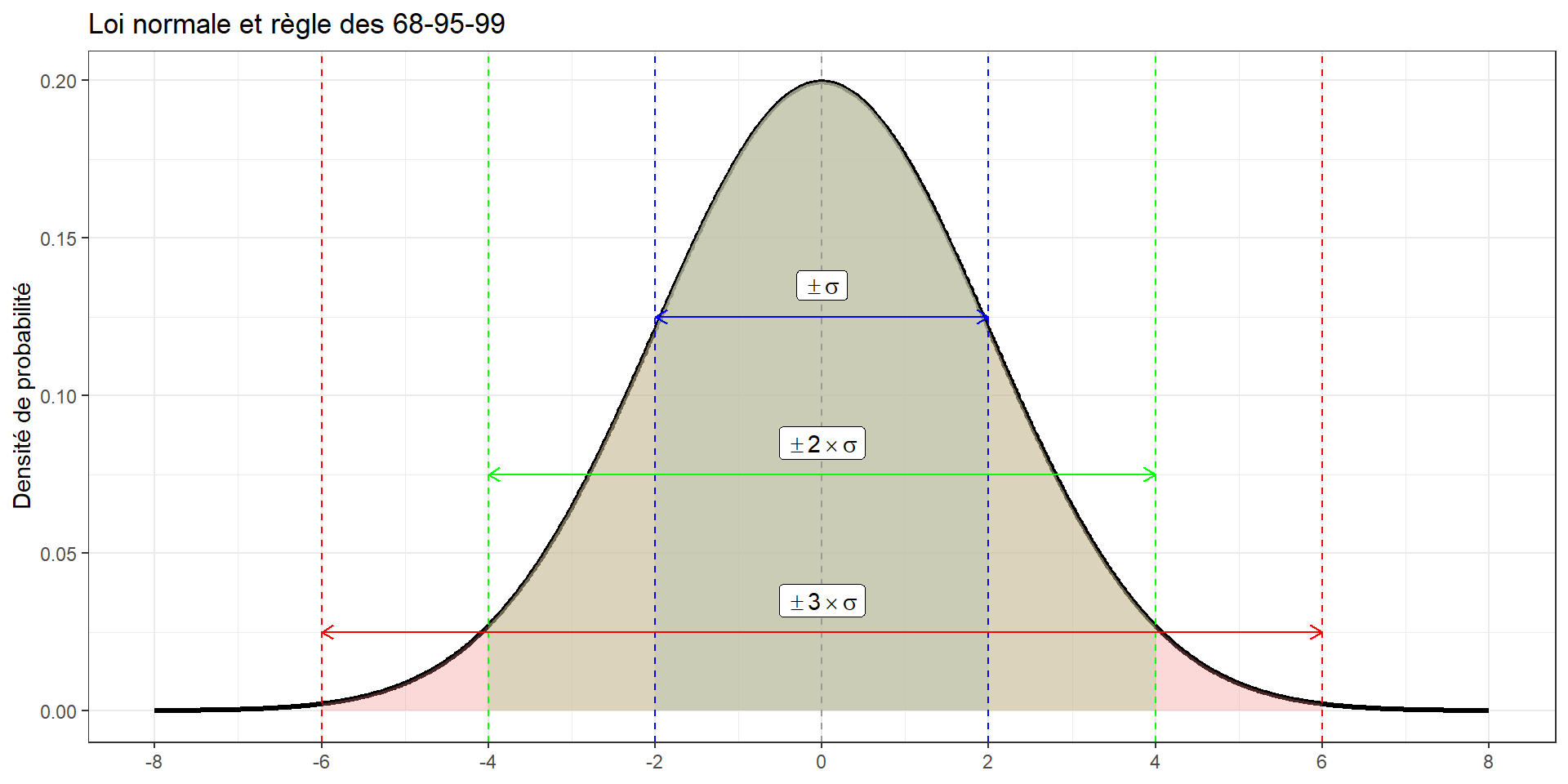
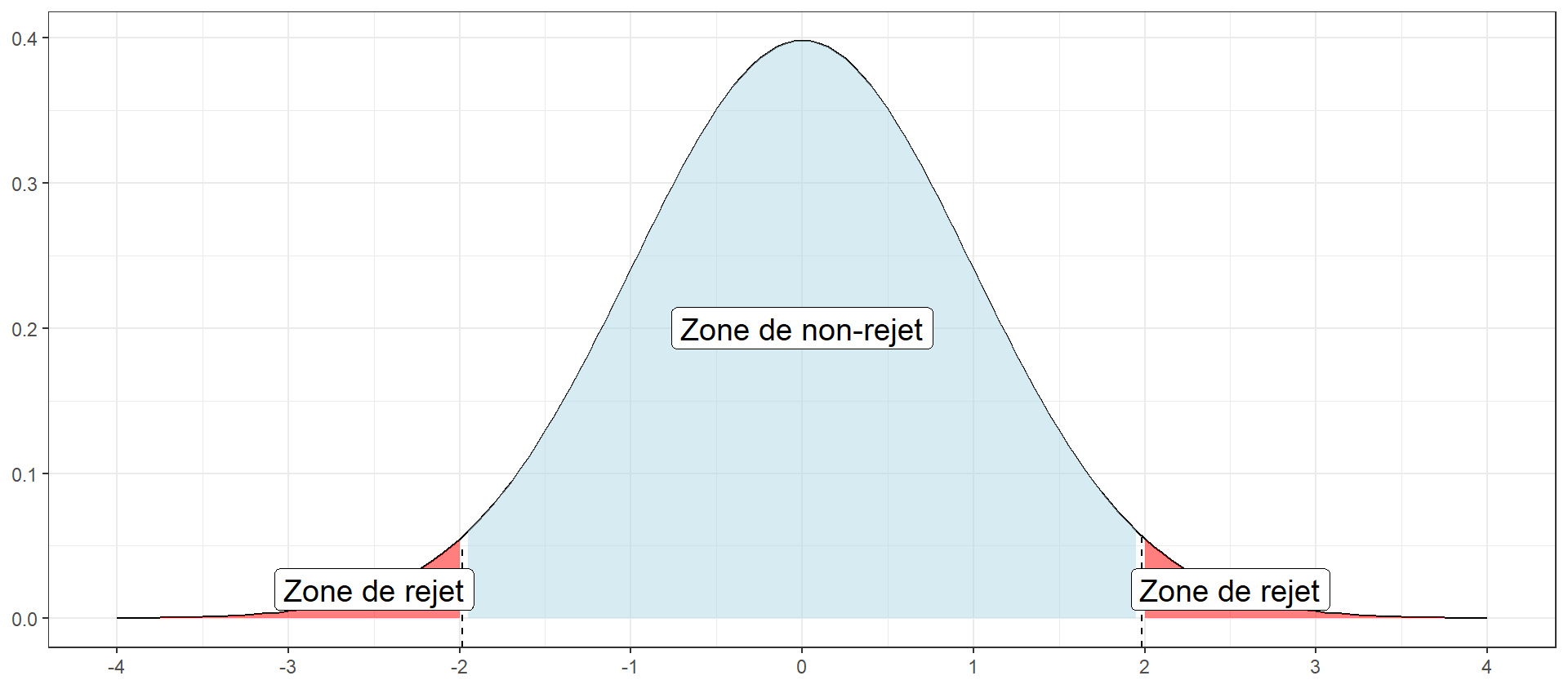
Loi normale et règle des 68-95-99
- Loi normale : Distribution en forme de cloche centrée autour de la moyenne.
- Règle 68-95-99 :
- 68% des données se trouvent à ±1 écart-type (σ) de la moyenne.
- 95% à ±2 écarts-types.
- 99.7% à ±3 écarts-types.
Illustration de la règle 68-95-99
Rappel: Théorème central limite
La moyenne ˉX de n valeurs issues d’une variable X de loi quelconque, de moyenne μ et de variance σ2, suit la loi (si n>30 ou X∼N)
ˉX∼N(μ,σ2/n)et doncˉX−μ√σ2/n∼N(0,1)
- En pratique, σ2 rarement connu, et donc doit être estimé à partir de l’échantillon
- ⟹ augmente un peu l’incertitude ⟹ utilisation d’une loi de Student (n−1) degrés de liberté (plutôt qu’une loi normale) : ˉX−μ√S2/n∼T(n−1)
D’où l’intervalle de confiance de μ au niveau de confiance 95%:
[ ˉx−s√nt1−α/2(n−1) ; ˉx+s√nt1−α/2(n−1) ]
Intervalle de confiance vers test de conformité
- On suppose / connaît ˉX−μ√S2/n∼T(n−1).
- On peut maintenant tester si la moyenne est égale à une valeur particulière, par ex est-ce que μ=100 ?
A partir d’un échantillon x, on peut calculer ˉx et s2 et se demander si la valeur est typique d’une loi de Student à n-1 ddl.
Quelques définitions
- H0 hypothèse nulle, H0:μ=100 vs H1 hypothèse alternative, H1:μ≠100
- Statistique de test: ˉX−μ√S2/n: il s’agit de la valeur qu’on peut calculer à partir de l’échantillon, et qu’on suppose suivre une certaine loi sous H0: ici une loi de Student à n−1 ddl
- p-value du test: probabilité calculée sous H0, que la statistique de test soit plus extrême que la valeur observée Tobs
p-value: “Dans un monde où H0 est vraie, la probabilité d’obtenir une valeur au moins aussi extrême pour la statistique de test est de p”
Si p < 0.05, on rejette l’hypothèse H0 au seuil de 5%
Dans notre cas, n = 112, donc T est censée suivre une loi de Student à 111 ddl, sous H0:
One Sample t-test
data: ozone$maxO3
t = -3.6406, df = 111, p-value = 0.0004148
alternative hypothesis: true mean is not equal to 100
95 percent confidence interval:
85.02578 95.58136
sample estimates:
mean of x
90.30357 [1] 0.0004147533Pour une loi de Student à n-1 ddl, -3.64 est une valeur peu probable donc on rejette H0, au seuil de 5%.
Comparaison de 2 moyennes (1/2)
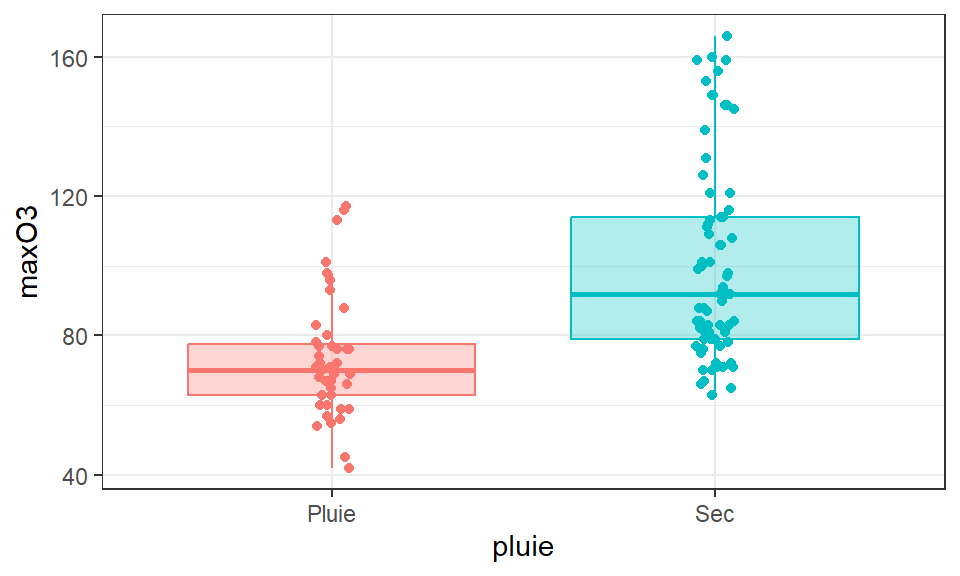
Question: le temps (sec/pluvieux) a-t-il un effet sur le max d’ozone ?
Réflexe: visu !
Passer de l’échantillon à n’importe quel jour induit de l’incertitude. Mais, il est plus facile de conclure qu’il y a une différence entre les deux moyennes dans la population si:
- Les moyennes sont très différentes ( vs )
- La variabilité du maximum d’ozone est faible au sein des jours pluvieux et au sein des jours secs
- Il y a beaucoup de données
Comparaison de 2 moyennes (2/2)
On considère que les données de la sous-population 1 sont telles que (Xi1)1≤i≤n1∼N(μ1,σ2) et que les données de la sous-population 2 sont telles que (Xi2)1≤i≤n2∼N(μ2,σ2) ⇒ (pour l’instant) seules les moyennes peuvent être différentes
- H0 hypothèse nulle, H0:μ1=μ2 vs H1 hypothèse alternative, H1:μ1≠μ2
- Statistique de test: T=¯X1−¯X2√ˆσ2n1+ˆσ2n2
- Sous H0, T suit une loi de Student n1+n2−2
Si les variances sont inégales, le test est différent ⟹ tester l’égalité des variances avant de faire le test de comparaison de moyennes
Test de comparaison de 2 variances
- H0 hypothèse nulle, H0:σ21=σ22 vs H1 hypothèse alternative, H1:σ21≠σ22
⟺ H0:σ21σ22=1 contre H1:σ21σ22≠1
- Statistique de test: F=S21S22
- Sous H0, F suit une loi de Fisher à n1−1 et n2−1 ddl
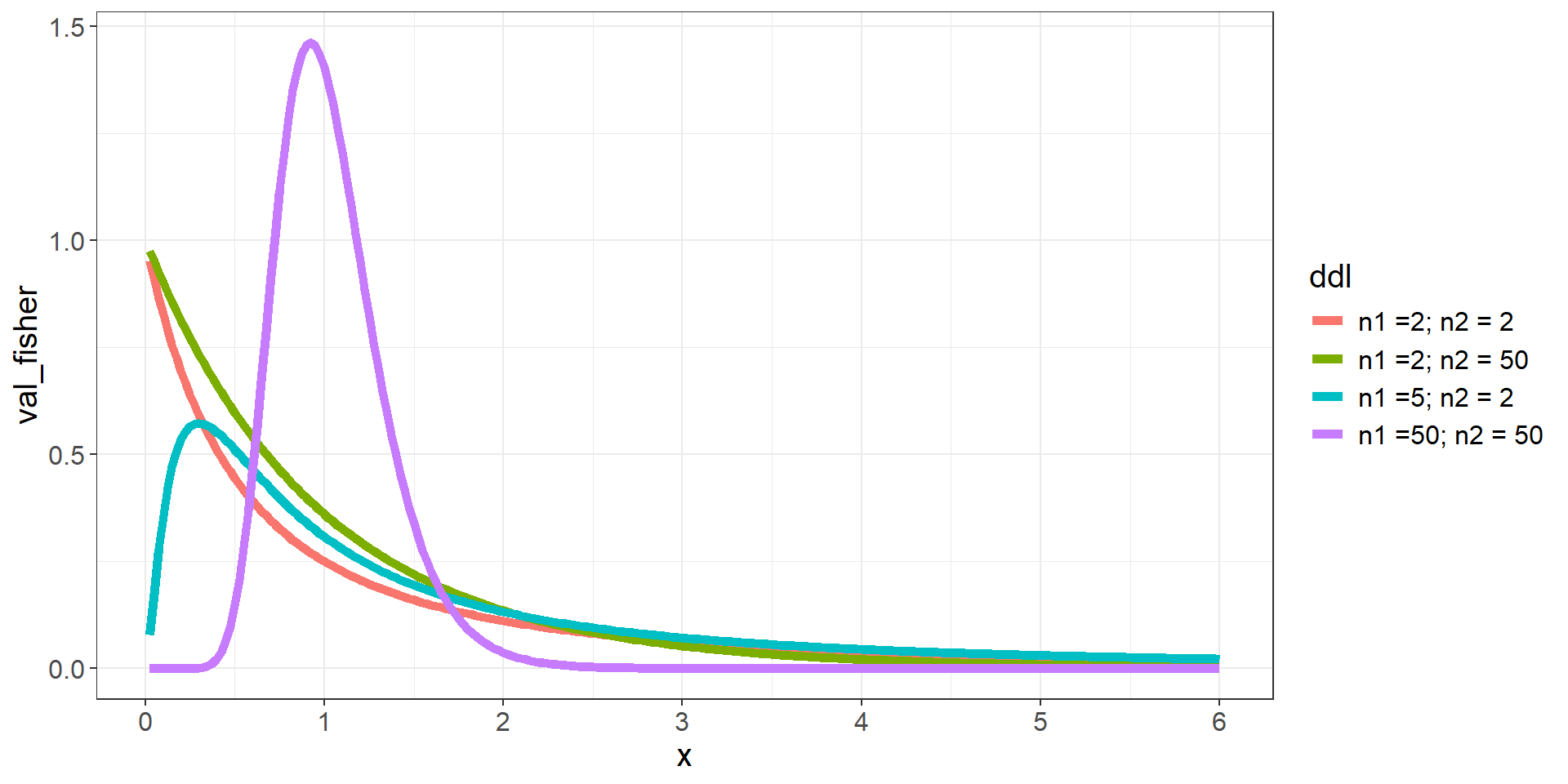
Mise en pratique
F test to compare two variances
data: maxO3 by pluie
F = 0.35906, num df = 42, denom df = 68, p-value = 0.0005659
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.2108847 0.6338374
sample estimates:
ratio of variances
0.3590605 Ici on rejette H0 au seuil de 5%, les variances sont différentes
Welch Two Sample t-test
data: maxO3 by pluie
t = -6.3362, df = 109.88, p-value = 5.321e-09
alternative hypothesis: true difference in means between group Pluie and group Sec is not equal to 0
95 percent confidence interval:
-36.02936 -18.86110
sample estimates:
mean in group Pluie mean in group Sec
73.39535 100.84058 On rejette H0, on affirme que les moyennes sont significativement différentes
Erreur et puissance d’un test
Décision d’un test prise pour la population (“il y a plus d’ozone les jours sec”) alors qu’on n’observe qu’un échantillon
⇒ Décision incertaine, et deux erreur possibles
- Erreur de première espèce: rejeter H0 alors que celle-ci est vraie: faux positif
- Erreur de deuxième espèce : ne pas rejeter H0 alors que celle-ci est fausse: faux négatif
En image ( qu’est-ce que H0 ici ?):

un test est dit puissant si son erreur de 2ème espèce est petite. La puissance d’un test est la probabilité de rejeter H0 et d’avoir raison
Puissance d’un test (1/2)
Question souvent posée Combien de données faut-il pour tester une différence entre 2 moyennes ?
Par ex.: combien de patients pour tester s’il y a une diff entre 2 médicaments pour faire baisser le taux de cholestérol ?
Rappel: de quoi est-ce que ça dépend ?
Reformuler la question
Combien faut-il de patients pour mettre en évidence une différence d’au moins 0.2g/l entre les 2 médicaments ?
Toujours pas possible
MAAAAAIS
Puissance d’un test (2/2)
MAAAAAIS si;
- on connaît la variance de la variable d’intérêt (ex. expériences antérieures montrent un écart-type de 0.4g/l) (
sd) - on veut détecter une différence donnée par ex toute diff > 0.2g/l (
delta) - on veut détecter cette différence avec proba de 80% (
power)
alors c’est possible
Analyse de variance à un facteur
Test de l’effet d’un facteur
Par ex. la direction du vent a-t-elle un effet sur le maximum d’ozone ?
Variable réponse quantitative, notée Y: maxO3
Variable explicative qualitative à I modalités (groupes): direction du vent
C’est le cadre de l’ANOVA (ANalysis Of VAriance)
maxO3 vent
87 Nord
82 Nord
92 Est
114 Nord
94 Ouest
80 OuestRéflexe …
Visu!
Question de base modifiée en : la moyenne du maximum d’ozone est-elle la même pour chaque direction du vent ?
Problématique qui revient souvent
- L’effet de cultures intermédiaires est-il le même selon l’espèce/variété ?
- La présence de haies a-t-elle une influence sur la population d’auxiliaires de cultures ?
Y a-t-il un effet de la variété sur le rendement du blé dans telle expérimentation ?
etc. etc. etc.
De manière générale, l’ANOVA est le cadre d’analyse de l’effet d’une variable qualitative à I modalités (par ex. sol nu / moutarde / phacélie) sur une variable quantitative
Mais alors pourquoi parler d’Analyse de Variance si on veut comparer des moyennes ?
La réponse viendra avec les explications (et les mains dans le cambouis)
Mettons les mains dans le cambouis
Données & notations
| vent | maxO3 | Notation |
|---|---|---|
| Est | 92 | y11 |
| Est | 121 | y12 |
| Nord | 87 | y21 |
| Nord | 82 | y22 |
| Ouest | 94 | y31 |
| Ouest | 80 | y32 |
| Sud | 90 | y41 |
| … | … | … |
yij valeur de Y pour l’individu j du groupe i
Moyenne du groupe i: yi∙=1ni∑nij=1yij
Moyenne générale : y∙∙=1n∑Ii=1∑nij=1yij
Comparaison de I moyennes
- Dans chaque groupe, on considère que les données suivent une loi N(μi,σ2)
On considère le MEME σ2.
Y1j∼N(μ1,σ2) peut s’érire Y1j=μ1+ε1j avec ε1j∼N(0,σ2)
Y2j∼N(μ2,σ2) peut s’écrire Y2j=μ2+ε2j avec ε2j∼N(0,σ2)
… …
YIj∼N(μI,σ2) peut s’écrire YIj=μI+εIj avec εIj∼N(0,σ2)
⇒ On peut résumer tout ça dans un seul modèle:
{∀i,j Yij=μi+εij∀i,j L(εij)=N(0,σ2)∀(i,j)≠(i′,j′) cov(εij,εi′j′)=0
Deux définitions du modèle
Si Yij est la valeur de la réponse du jeme individu (j=1,...,ni) du ieme groupe (i=1,...,I):
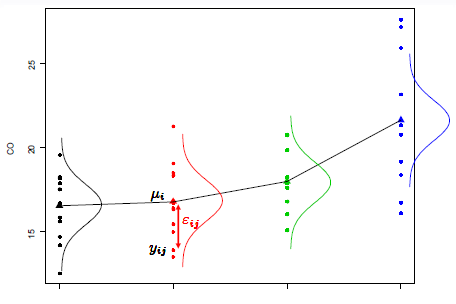
{∀i,j Yij=μi+εij∀i,j L(εij)=N(0,σ2)∀(i,j)≠(i′,j′) cov(εij,εi′j′)=0
I paramètres: les μi
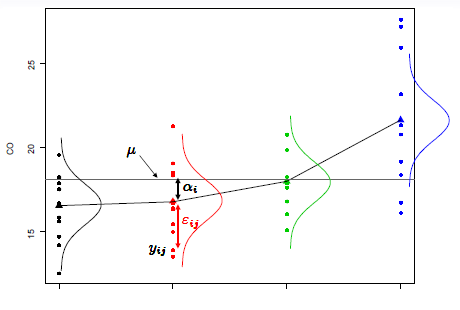
{∀i,j Yij=μ+αi+εij∀i,j L(εij)=N(0,σ2)∀(i,j)≠(i′,j′) cov(εij,εi′j′)=0
I+1 paramètres: l’effet moyen μ et les I coefficients αi (effet du niveau i)
On doit avoir ∀ i, μ+αi=μi besoin de contraintes
Estimer les paramètres du modèle
On minimise les écarts entre observations (Yij) et prédictions par le modèle ˆYij.
On minimise le critère des moindres carrés ordinaires (: pourquoi carré 2 ?)
SCER=I∑i=1ni∑j=1(Yij−ˆYij)2=I∑i=1ni∑j=1(Yij−(ˆμ+ˆαi))2
SCER minimal quand ∀ i, ˆμ+ˆαi=1nini∑j=1Yij=Yi∙
Contraintes classiques:
Un niveau particulier comme référence: α1=0 ⇒ˆμ=Y1∙ et ∀i,ˆαi=Yi∙−Y1∙
la moyenne des moyennes par groupe comme référence: ∑Ii=1αi=0 ⇒ˆμ=1I∑Ii=1Yi∙, ∀i,ˆαi=Yi∙−ˆμ
Exemple pour clarifier
| groupe 1 | groupe 2 | groupe3 | |
|---|---|---|---|
| y11=6 | y21=2 | y31=3 | |
| y12=9 | y22=4 | y32=1 | |
| y13=6 | y22=3 | ||
| y1∙=7 | y2∙=3 | y3∙=2 | y∙∙=4.25 |
Avec traitement 1 comme référence : ˆμ=7; ˆα1=0; ˆα2=−4 et ˆα3=−5
∑Ii=1αi=0 : ˆμ=13(7+3+2)=4 ; ˆα1=3 ; ˆα2=−1 et ˆα3=−2
Important
Le choix de la contrainte impacte FORTEMENT l’interprétation
- ∑iαi=0, la comparaison est faite par rapport à la moyenne des moyennes par modalité
- α1=0, la comparaison est faite par rapport à un niveau de ref (moins intuitif, et pas pratique quand présence d’interactions)
Certaines fonctions de R par défaut utilisent la contrainte 2. !
Comparez les sorties de ces différentes lignes de code…
Variance résiduelle
Valeurs prédites: ˆyij=ˆμ+ˆαi=yi∙
Erreurs d’ajustement ou résidus : ˆεij=yij−ˆyij=yij−yi∙
Estimateur de la variabilité résiduelle σ2:
ˆσ2=∑ij(Yij−Yi∙)2n−I=∑ijˆε2ijn−I E(ˆσ2)=σ2
n−I degrés de liberté sont associés à la somme des carrés des résidus du modèle.
Décomposition de la variabilité
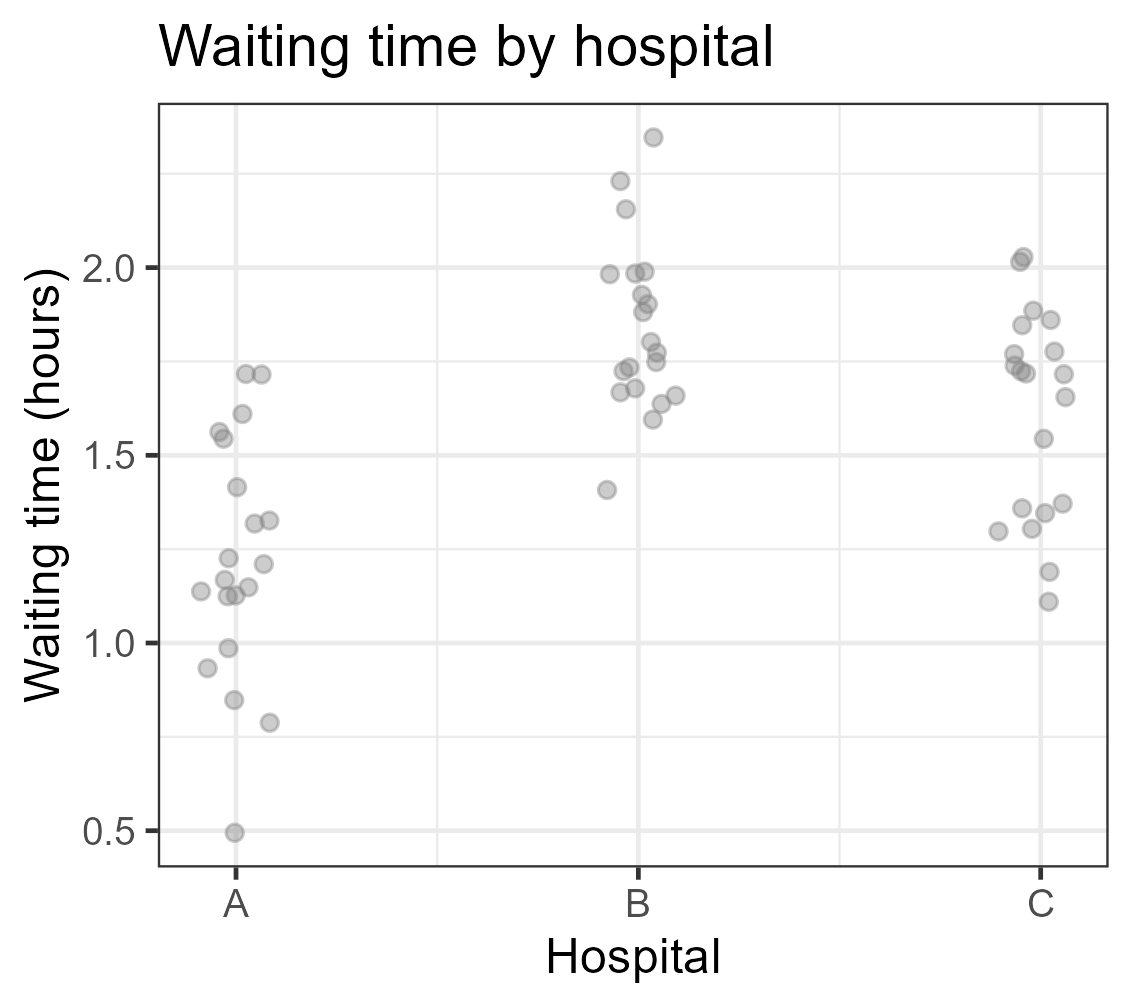
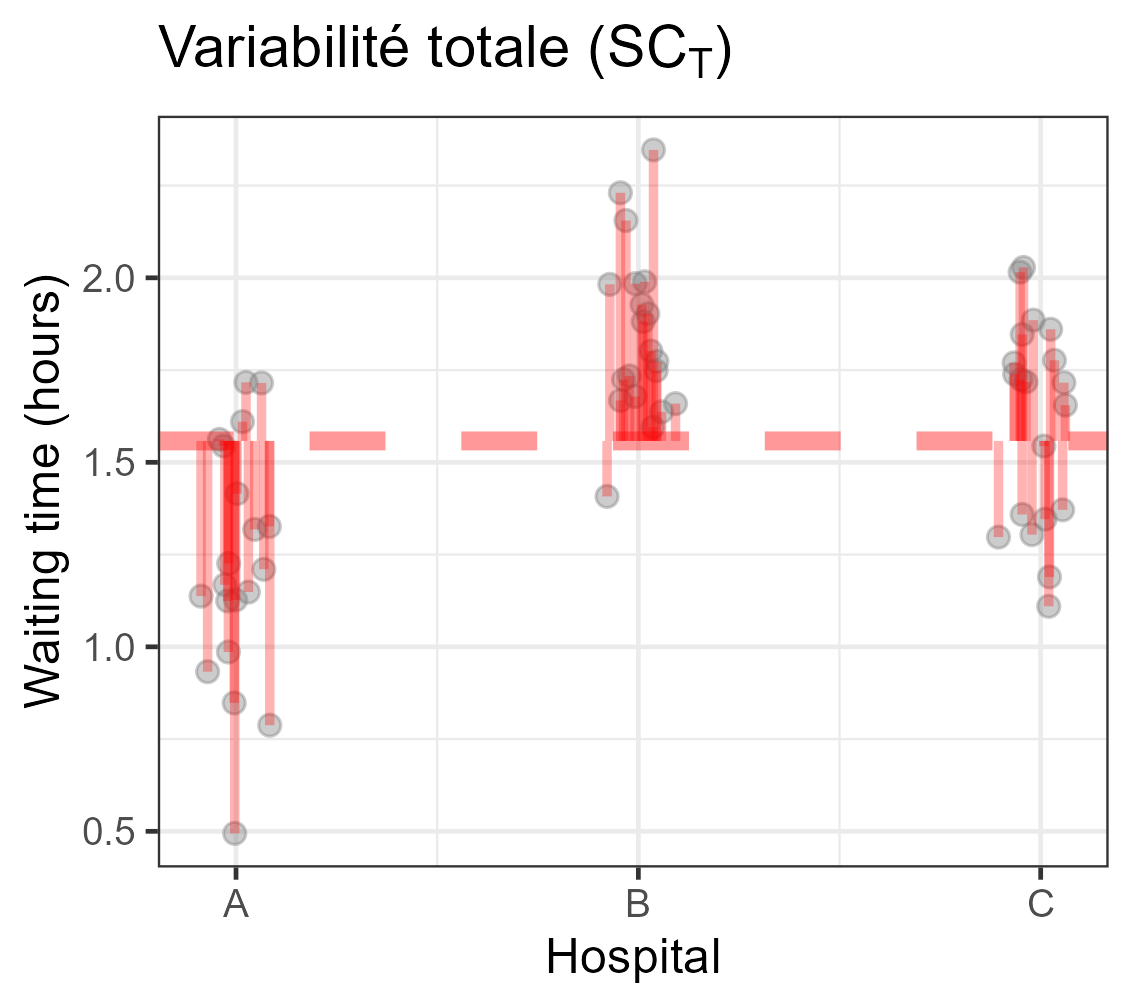
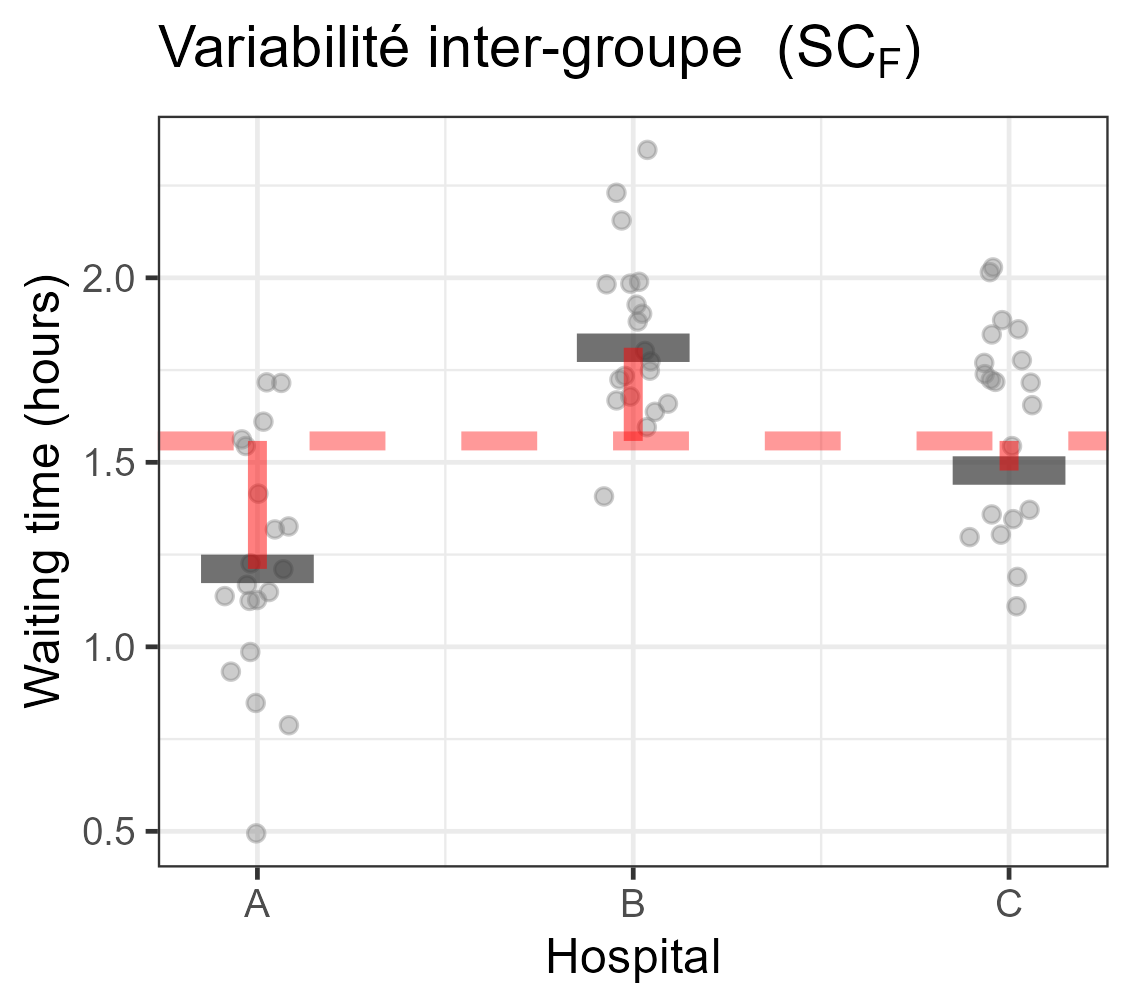
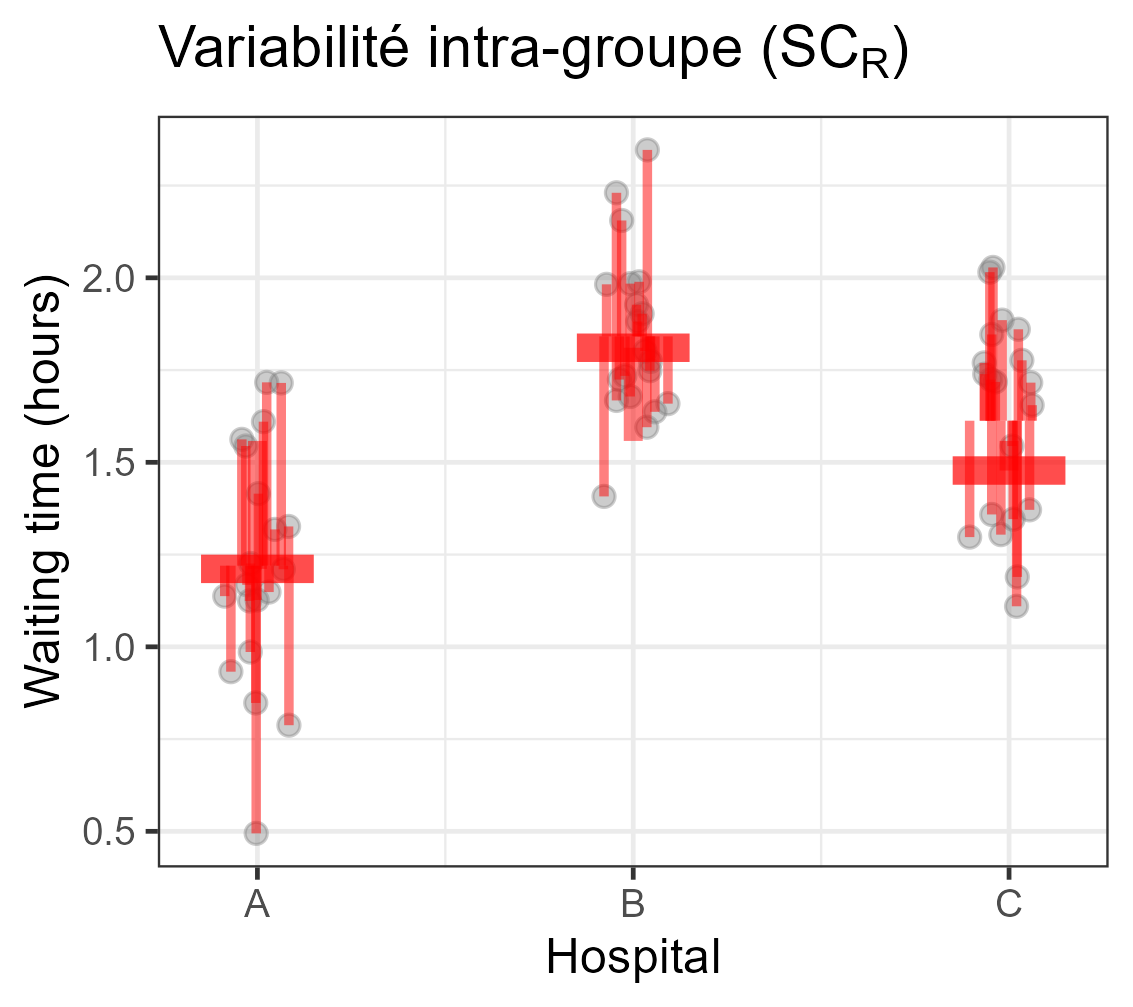
Equation d’analyse de la variance
| ∑i,j(Yij−Y∙∙)2⏟SCT | =∑ini(Yi∙−Y∙∙)2⏟SCF | +∑i,j(Yij−Yi∙)2⏟SCR | |
| Variabilité | totale | modèle | résiduelle |
| ddl | n−1 | I−1 | n−I |
- Vous pouvez commencez à comprendre d’où vient le nom ANalysis Of VAriance
Indicateur de liaison : rapport de corrélation
η2=SCmodèleSCtotal=1−SCrésiduelleSCtotal
Expliqué à mon grand-père (ou presque): la proportion de variabilité du phénomène que mon modèle explique
Propriétés:
- 0≤η2≤1 (obvious)
- η2=0⇔SCmodèle=0
- η2=1⇔SCmodèle=SCtotal
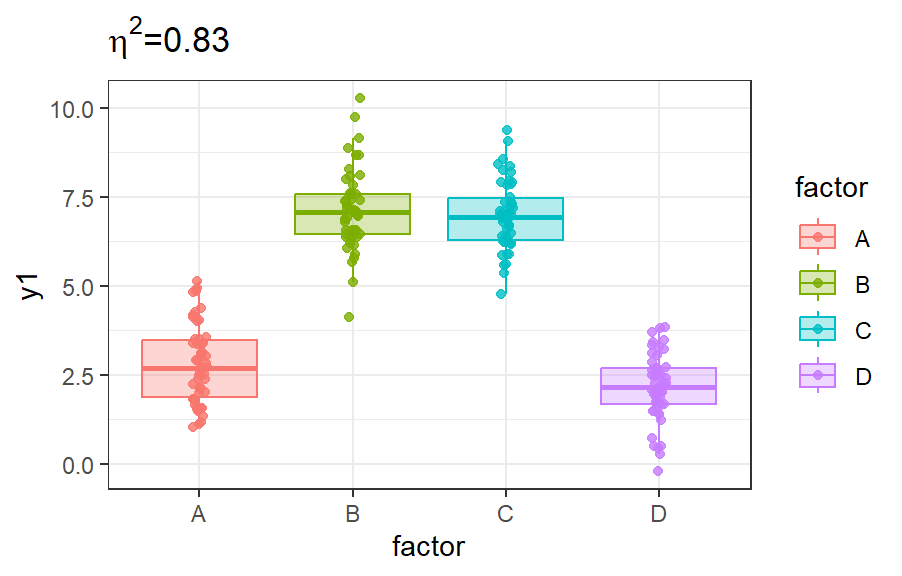
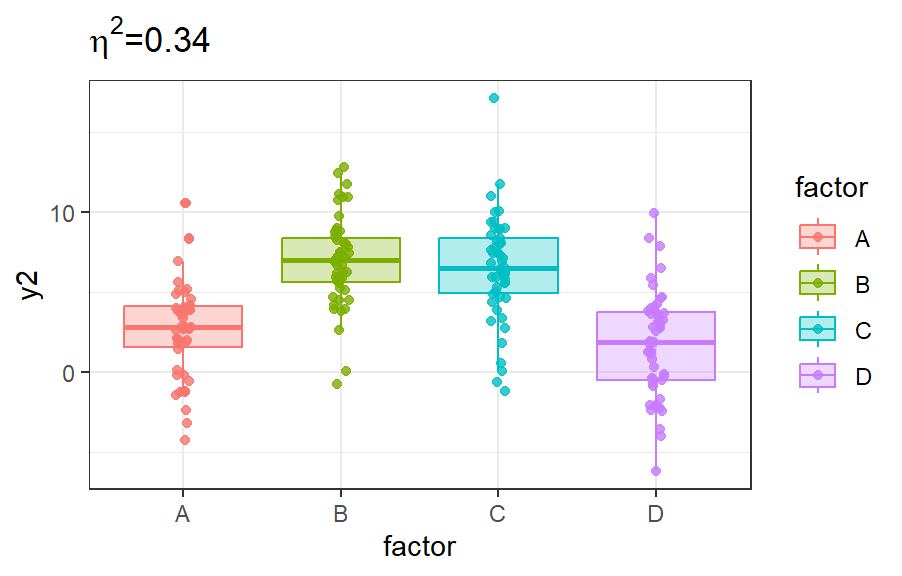
Deux rapports de corrélation différents pour des Yi∙ identiques.
Inférence: test global
Rappel de l’objectif: y a-t-il un effet du facteur sur Y ?
→ La variabilité de Y est-elle expliquée par le facteur groupe ? Ou bien peut-on considérer que les données proviennt d’une même loi N(μ,σ2) ?
Hypothèses:
H0: ∀i, μi=μ H1: ∃i / μi≠μ
⇔
H0: ∀i, αi=0 H1: ∃i / αi≠0
On a : E(SCmodI−1)=σ2+1I−1I∑i=1niα2i;E(SCRn−I)=σ2
Statistique de test : Fobs=SCmod/(I−1)SCR/(n−I)
Loi de Fobs sous H0 : L(Fobs)=FI−1n−I
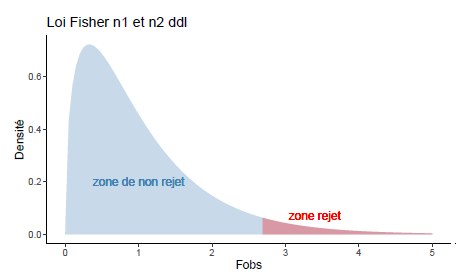
Table d’analyse de variance: décomposition de variabilité et test
- Ce qui est souvent reporté dans le cadre d’une ANOVA
| Variabilité | Somme Carrés | ddl | Carré moyen | Fobs |
|---|---|---|---|---|
| Facteur | ∑ini(Yi∙−Y∙∙)2 | I−1 | SCFI−1 | CMFCMR |
| Résiduelle | ∑i,j(Yij−Yi∙)2 | n−I | SCRn−I | |
| Totale | ∑i,j(Yij−Y∙∙)2 | n−1 |
Call:
LinearModel(formula = maxO3 ~ vent, data = ozone)
Residual standard error: 27.32 on 108 degrees of freedom
Multiple R-squared: 0.08602
F-statistic: 3.388 on 3 and 108 DF, p-value: 0.02074
AIC = 744.8 BIC = 755.7
Ftest
SS df MS F value Pr(>F)
vent 7586 3 2528.69 3.3881 0.02074
Residuals 80606 108 746.35
Ttest
Estimate Std. Error t value Pr(>|t|)
(Intercept) 94.7382 3.0535 31.0265 < 2e-16
vent - Est 10.8618 6.8294 1.5904 0.11466
vent - Nord -8.6092 4.6219 -1.8627 0.06522
vent - Ouest -10.0382 4.0972 -2.4500 0.01589
vent - Sud 7.7856 5.2052 1.4957 0.13764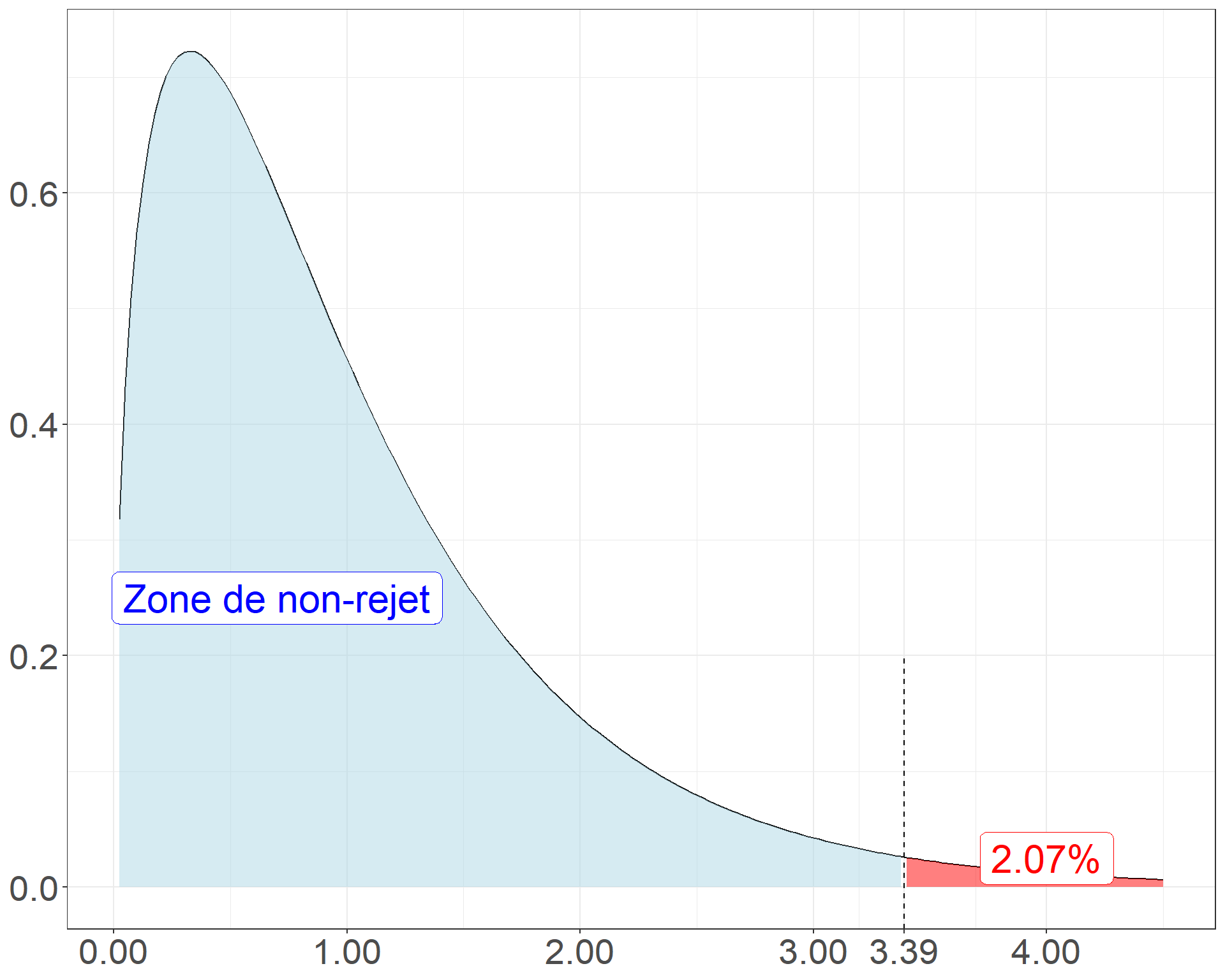
Inférence: test de conformité d’un coefficient (1/2)
Si on rejette l’hypothèse H0:∀i,αi=0, on veut savoir quels αi sont différents de 0
La valeur de ˆαi dépend de l’échantillon de données et donc l’estimateur ˆαi est une variable aléatoire L(ˆαi)=N(αi,σ2ˆαi) ⟺ L(ˆαi−αiσˆαi)=N(0,1)
L(ˆαi−αiˆσˆαi)=Tn−I
On peut donc construire le test de nullité d’un coefficient (α1 par exemple):
Hypothèses : H0:α1=0 contre H1:α1≠0
Statistique de test ˆα1ˆσˆα1
Loi de la statistique de test sous H0 L(Tobs=ˆα1ˆσˆα1)=Tν=n−I
Décision par la p-value
Rq : connaissant la loi de ˆα1, on peut construire un intervalle de confiance: α1∈[ˆα1−ˆσˆα1×t0.975(n−I) ; ˆα1+ˆσˆα1×t0.975(n−I)]
Inférence: test de conformité d’un coefficient (2/2)
Estimate Std. Error t value Pr(>|t|)
(Intercept) 94.738210 3.053461 31.026504 1.290980e-55
vent - Est 10.861790 6.829425 1.590440 1.146587e-01
vent - Nord -8.609178 4.621850 -1.862713 6.522029e-02
vent - Ouest -10.038210 4.097207 -2.450013 1.589160e-02
vent - Sud 7.785599 5.205173 1.495743 1.376372e-01 Estimate Std. Error t value Pr(>|t|)
(Intercept) 94.738210 3.053461 31.026504 1.290980e-55
vent - Est 10.861790 6.829425 1.590440 1.146587e-01
vent - Nord -8.609178 4.621850 -1.862713 6.522029e-02
vent - Ouest -10.038210 4.097207 -2.450013 1.589160e-02
vent - Sud 7.785599 5.205173 1.495743 1.376372e-01Test de comparaison 2 à 2
Autre stratégie : comparer toutes les paires de moyennes
Pb : on effectue beaucoup de tests ⇒ risque de multiplier les erreurs en rejetant des hypothèses H0.
⇒ correction des tests: modifier le seuil α=5% et prendre α=5%(nb tests)
⇒ les tests sont peu puissants
$adjMean
vent emmean SE df lower.CL upper.CL
Est 105.6 8.64 108 83.7 127.5
Nord 86.1 4.91 108 73.7 98.6
Ouest 84.7 3.86 108 74.9 94.5
Sud 102.5 5.96 108 87.4 117.7
Confidence level used: 0.95
Conf-level adjustment: bonferroni method for 4 estimates
$groupComp
$groupComp$Letters
Ouest Nord Sud Est
"a" "a" "a" "a"
$groupComp$LetterMatrix
a
Ouest TRUE
Nord TRUE
Sud TRUE
Est TRUE
attr(,"class")
[1] "meansComp"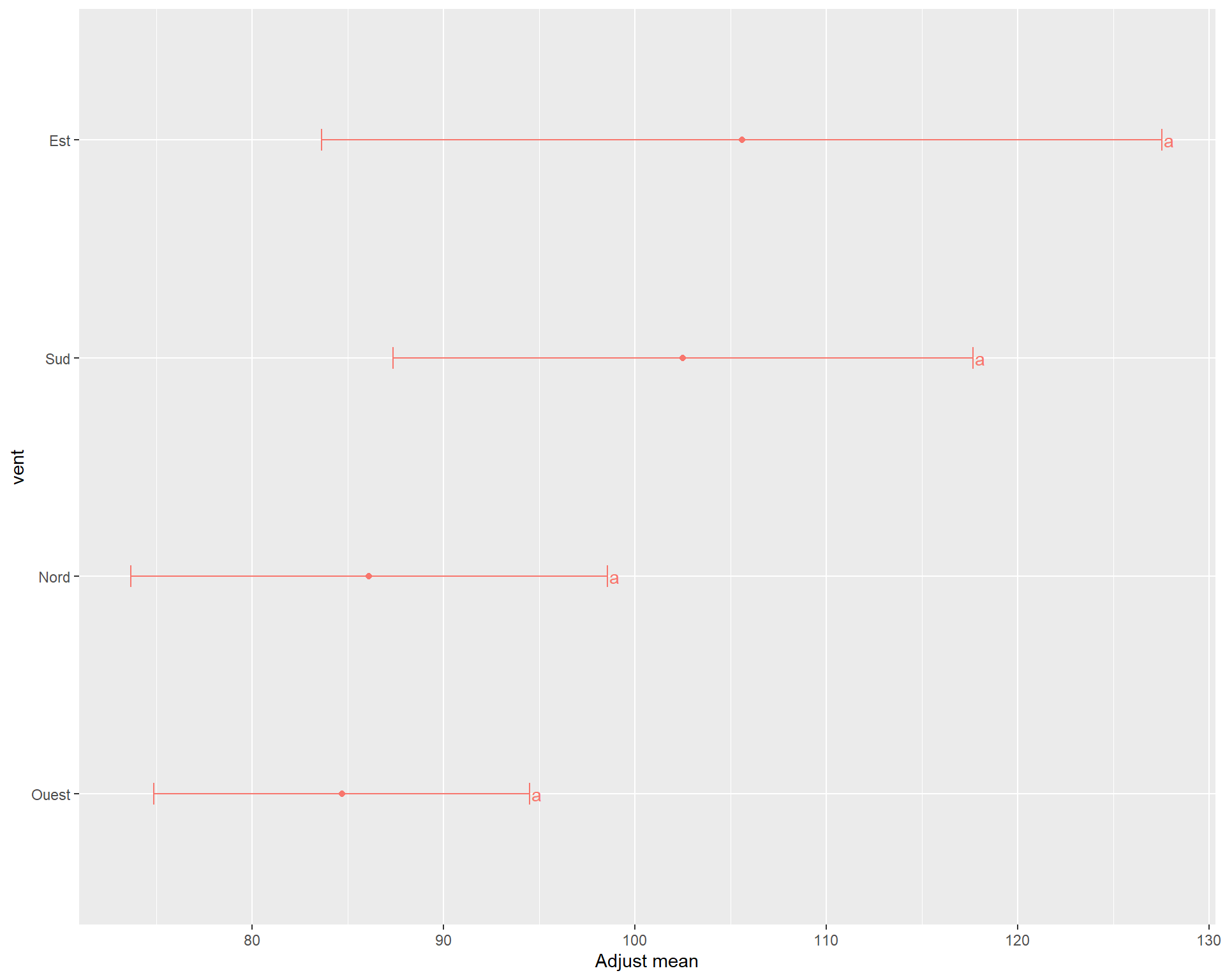
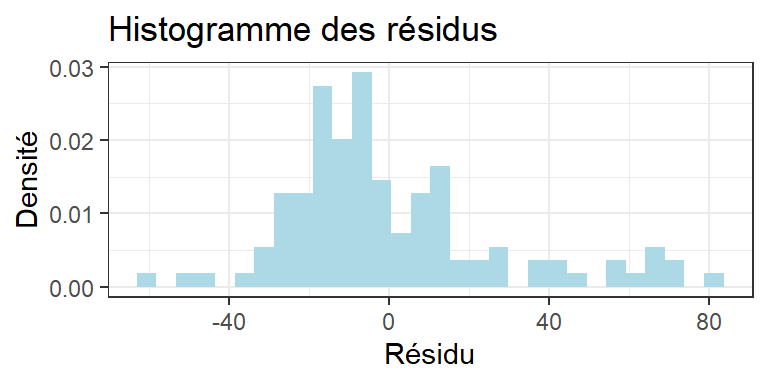
Analyse des résidus du modèle
Rappel du modèle:
{∀i,j Yij=μi+εij∀i,j L(εij)=N(0,σ2)∀(i,j)≠(i′,j′) cov(εij,εi′j′)=0
On a des hypothèses sur les résidus du modèle
Les résidus, c’est ce qui n’est pas expliqué par le modèle. Donc pour les estimer, il faut ajuster le modèle
On peut ensuite vérifier les hypothèses du modèle
Régression linéaire simple
Liaison linéaire
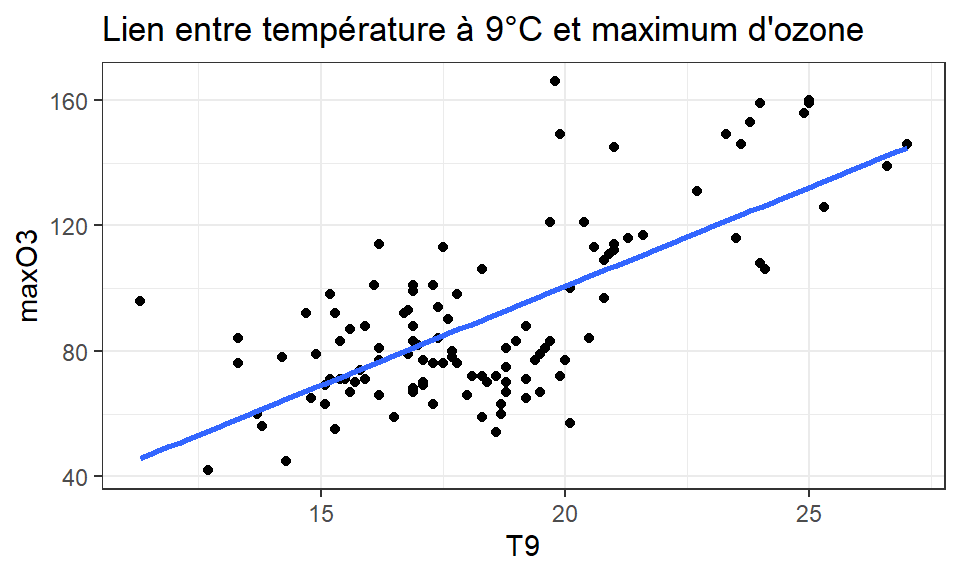
Questions
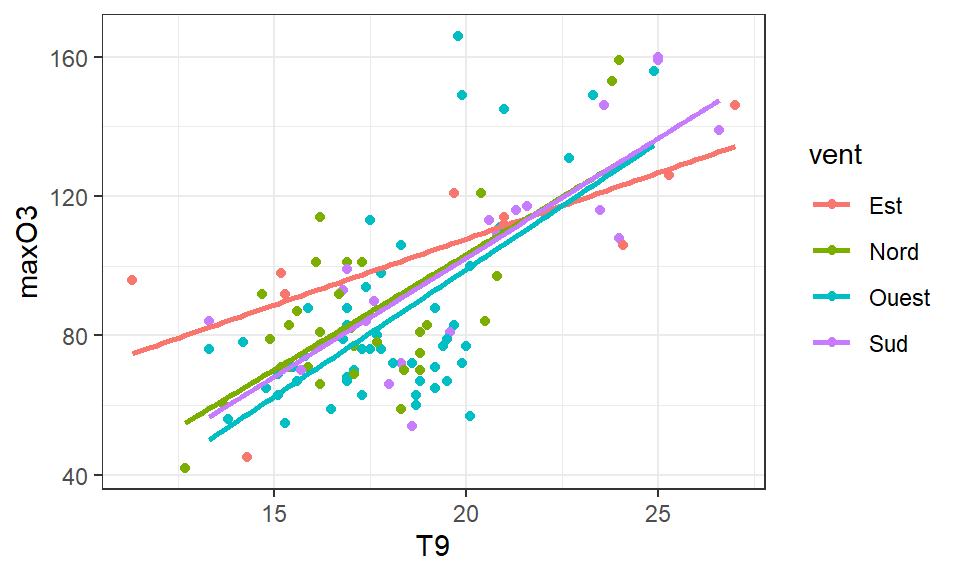
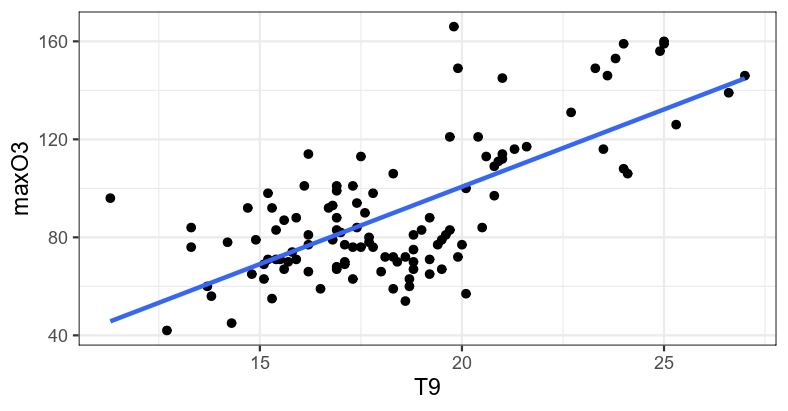
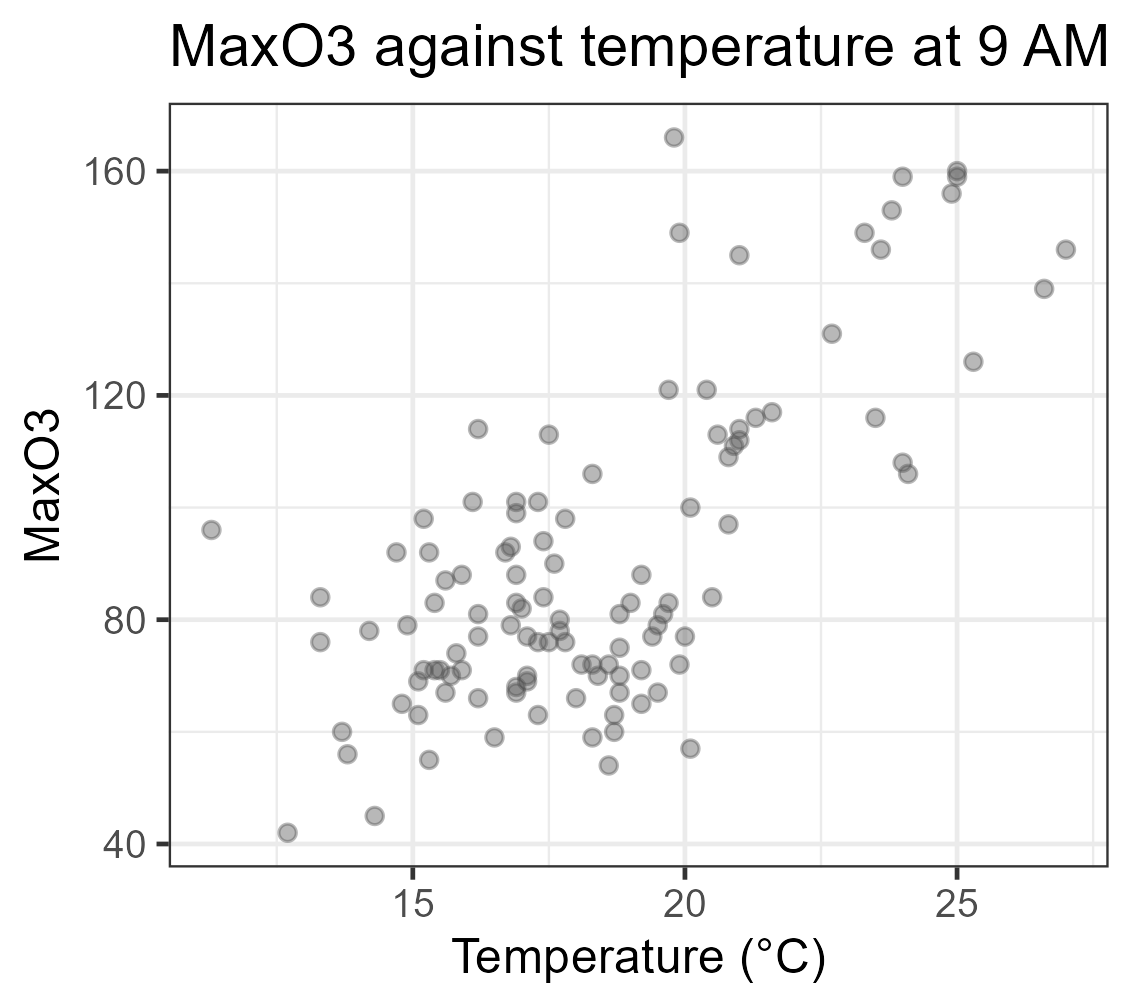
- Influence de la température sur le max d’ozone ?
- A quel max d’ozone peut-on s’attendre s’il fait 19.5°C à 9h ?
Objectifs
Etudier qualitativement et quantitativement la dépendance d’une variable réponse quantitative Y en fonction d’une variable quantitative x
La variable x permet elle d’expliquer la variabilité de la variable Y?
Prédire Y à partir de x
Un indice de liaison: le coefficient de corrélation linéaire
rxy=∑ni=1(xi−ˉx)(yi−ˉy)√∑ni=1(xi−ˉx)2√∑ni=1(yi−ˉy)2
- −1≤rxy≤1
- rxy=0⇔ pas de liaison linéaire entre X et Y
- rxy≈1⇔ relation linéaire croissante entre X et Y
- rxy≈−1⇔ relation linéaire décroissante entre X et Y
Pearson's product-moment correlation
data: ozone$maxO3 and ozone$T9
t = 10.263, df = 110, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.5904575 0.7832906
sample estimates:
cor
0.6993865 - rxy=0.70 ⇒ corrélation assez forte (et significativement différente de 0, mais on verra ça plus tard)
Corrélation, causalité etc. (1/2)
- Une corrélation est un indicateur utile, mais à utiliser avec précaution
“Corrélation n’implique pas causalité”
Oui, mais… la présence d’une corrélation suppose généralement un lien
- Ex. on observe une corrélation entre A et B. Plusieurs cas existent.
A ⇒ B (ex. ⇒ cancer )
B ⇒ A (idem)
A ⇒ B et ET B ⇒ A (ex. et CO2 )
Une variable C a été omise, et influence A et B. (ex. (C) ⇒ (A), (C) ⇒ (B), ⇔ )
Corrélation purement fortuite (site spurious correlations)
Corrélation, causalité etc. (2/2)
Ex. pour rigoler:
“Corrélation n’implique pas causalité”
Ok, mais cette affirmation ne doit pas servir à réfuter toute association constatée dans des données.
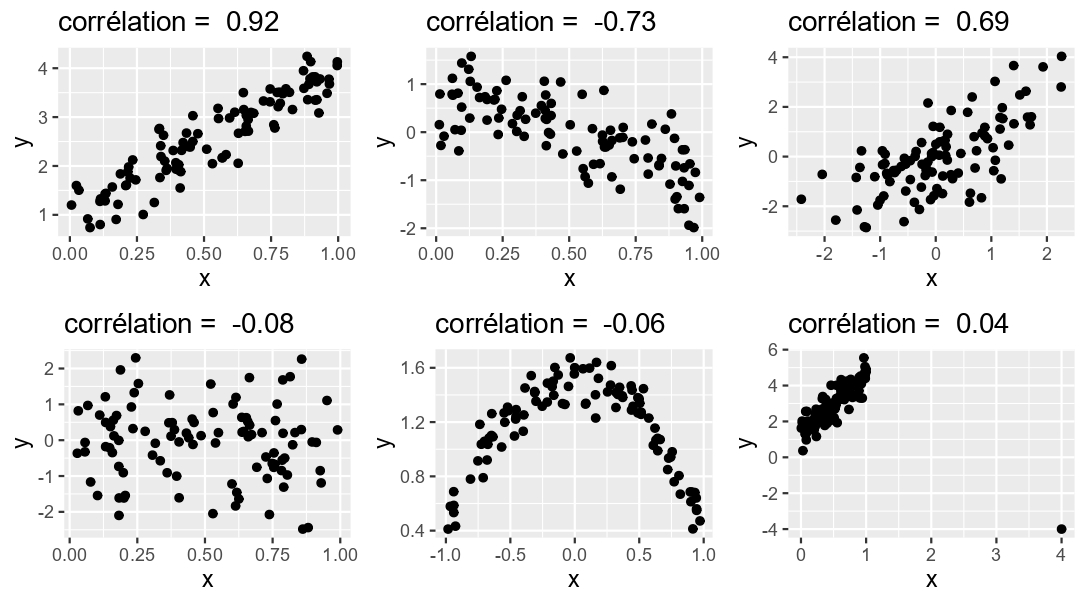
Quelques valeurs de corrélations
(Re)Mettons les mains dans le cambouis
Le modèle de régression linéaire simple s’écrit ainsi:
Yi=β0+β1xi+εi,εiind∼N(0,σ2), avec
- xi la valeur de la variable explicative pour l’observation i
- i=1,…,n le numéro d’individu, n le nombre total d’individus
- β0 l’ordonnée à l’origine
- β1 la pente de la droite, mesure de l’effet de la variable x
- σ2 la variance
Estimation des paramètres
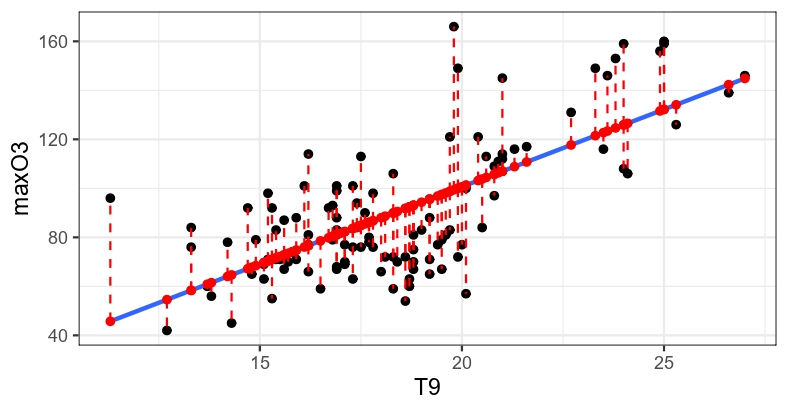
SCER=n∑i=1(yi−ˆyi)2=n∑i=1(yi−^β0−^β1xi)2
Paramètres d’espérance:
- ^β1=∑ni=1(xi−ˉx)(Yi−ˉY)∑ni=1(xi−ˉx)2
- ^β0=ˉY−^β1ˉx
Variance résiduelle:
ˆσ2=1n−2n∑i=1(Yi−ˆYi)2 ; ddlrésiduelle=n−2 ; E(ˆσ2)=σ2
Test de conformité
L(ˆβ1)=N(β1,σ2β1) avec σ2β1=σ2∑ni=1(xi−ˉx)2
⟹ L(ˆβ1−β1σˆβ1)=N(0,1) ⟹ L(ˆβ1−β1ˆσˆβ1)=Tn−2
On peut donc construire le test de nullité de β1:
Hypothèses : H0:"β1=0" contre H1:"β1≠0"
Statistique de test : ˆβ1ˆσˆβ1 Loi de la statistique de test sous H0: L(Tobs=ˆβ1ˆσˆβ1)=Tν=n−2
Rq 1. : comme dans l’ANOVA, connaissant la loi de ˆβ1, on peut construire un intervalle de confiance: β1∈[ˆβ1−ˆσˆβ1×t0.975(n−2) ; ˆβ1+ˆσˆβ1×t0.975(n−2)]
Rq 2. : on peut aussi tester β0 mais cela a moins d’importance en pratique
Décomposition de la variabilité
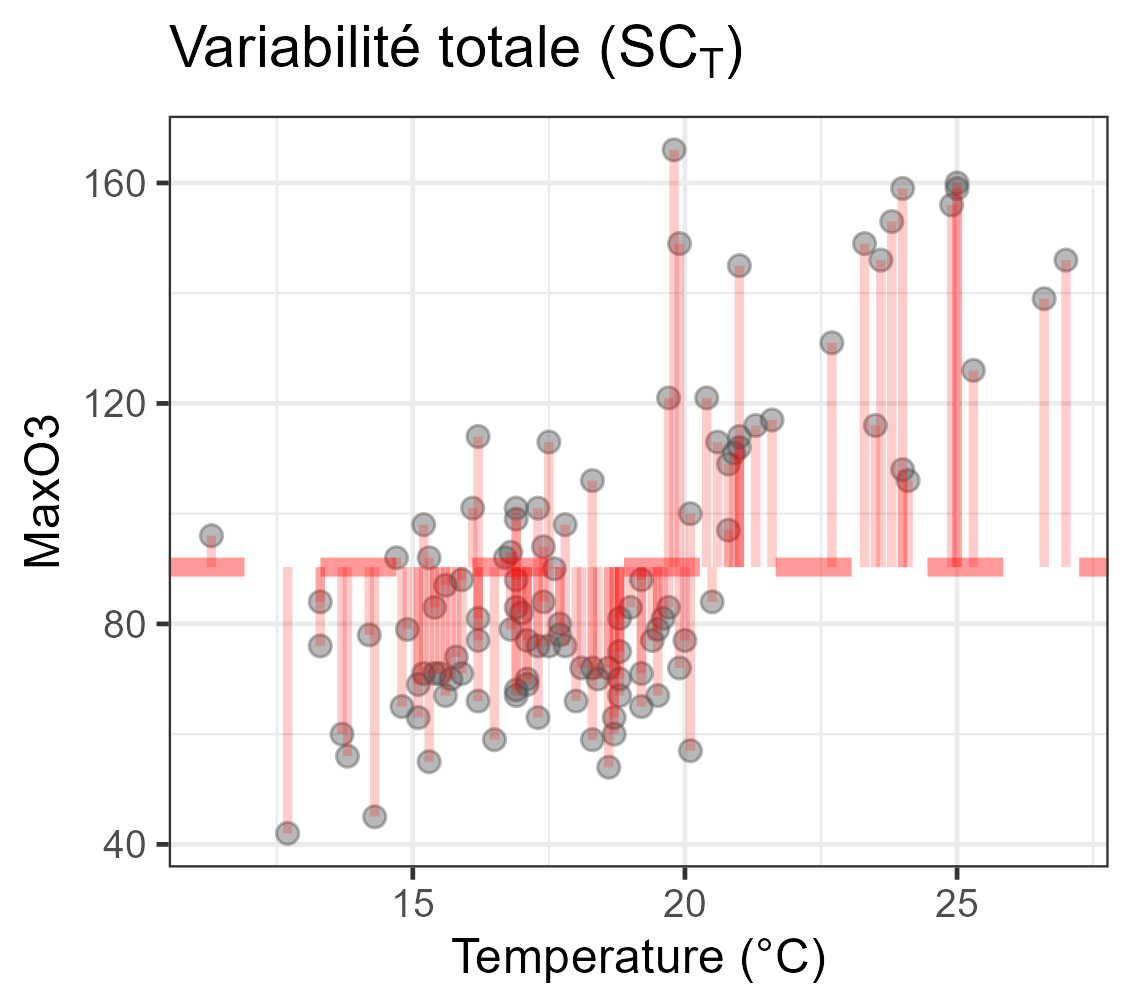
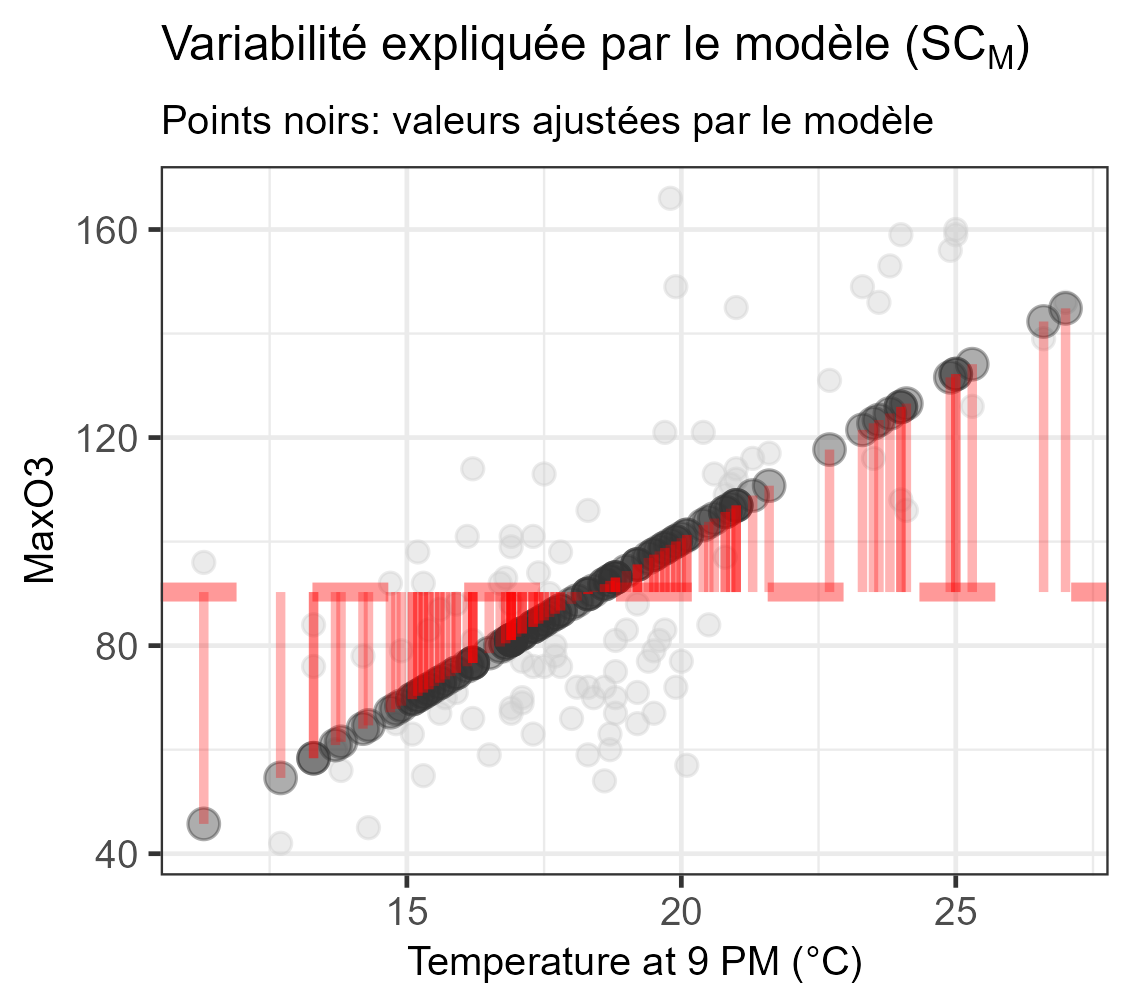
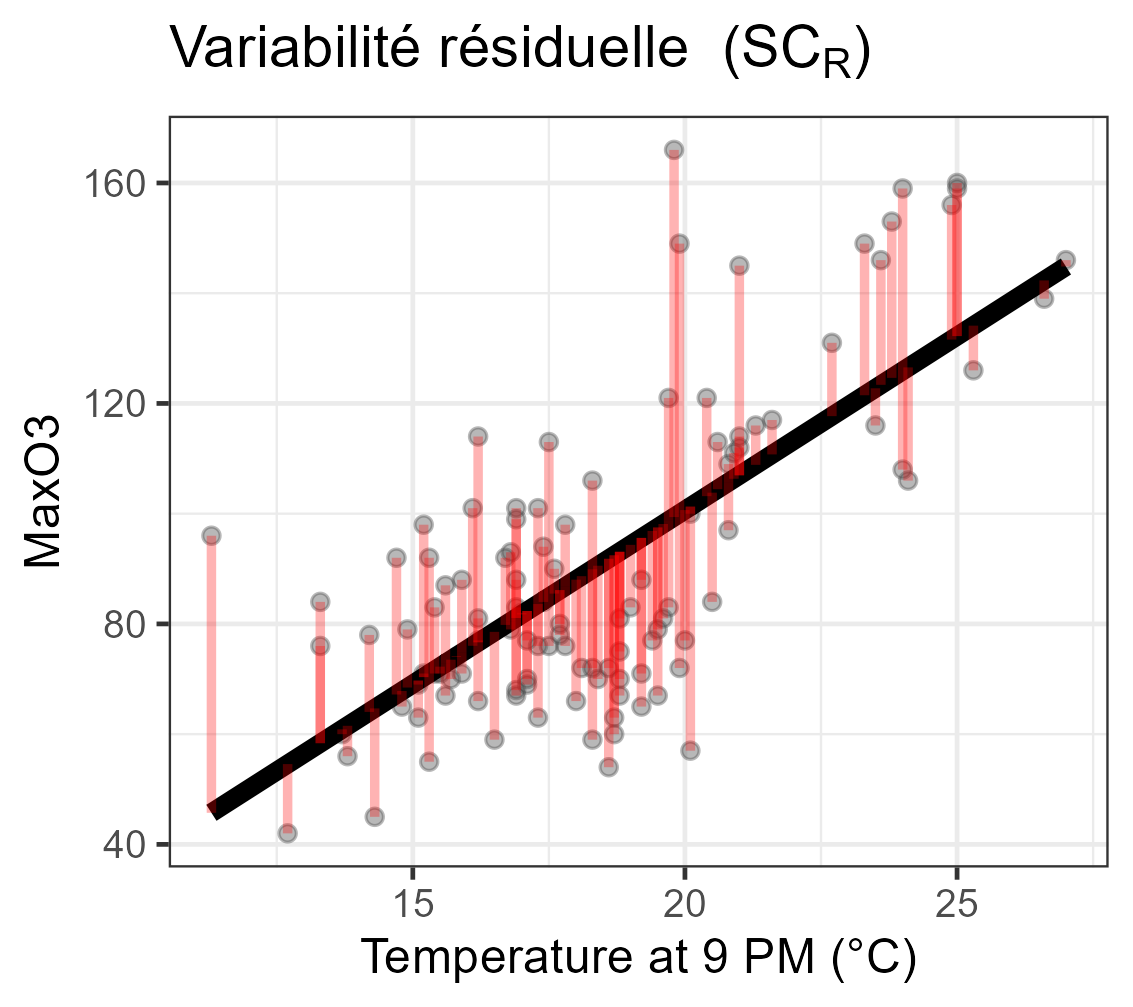
∑ni=1(Yi−ˉY)2=∑ni=1(ˆYi−ˉY)2+∑ni=1(Yi−ˆYi)2SCT=SCM+SCRn−1=1+n−2
Table d’analyse de la variance
| Source de variation | Somme des carrés | Degrés de liberté | Carré moyen | F |
|---|---|---|---|---|
| Modèle | SCM | 1 | SCM1 | CMMCMR |
| Erreur | SCR | n−2 | SCRn−2 | |
| Total | SCT | n−1 |
Comparaison de SCM et SCT par le critère R2=SCMSCT
Propriétés :
- 0≤R2≤1
- R2=0⇔SCmodéle=0
- R2=1⇔SCmodèle=SCtotal
Explication claire du concept sur le site de Science Etonnante
Test du modèle
Hypothèses
- H0:β1=0,⇔ le modèle n’a pas d’intérêt (x n’explique pas Y)
- H1:β1≠0,⇔ le modèle a un intérêt (x explique Y)
Stat de Fisher
F=SCM/1SCR/(n−2)
Loi de F sous H0:L(F)=F1n−2
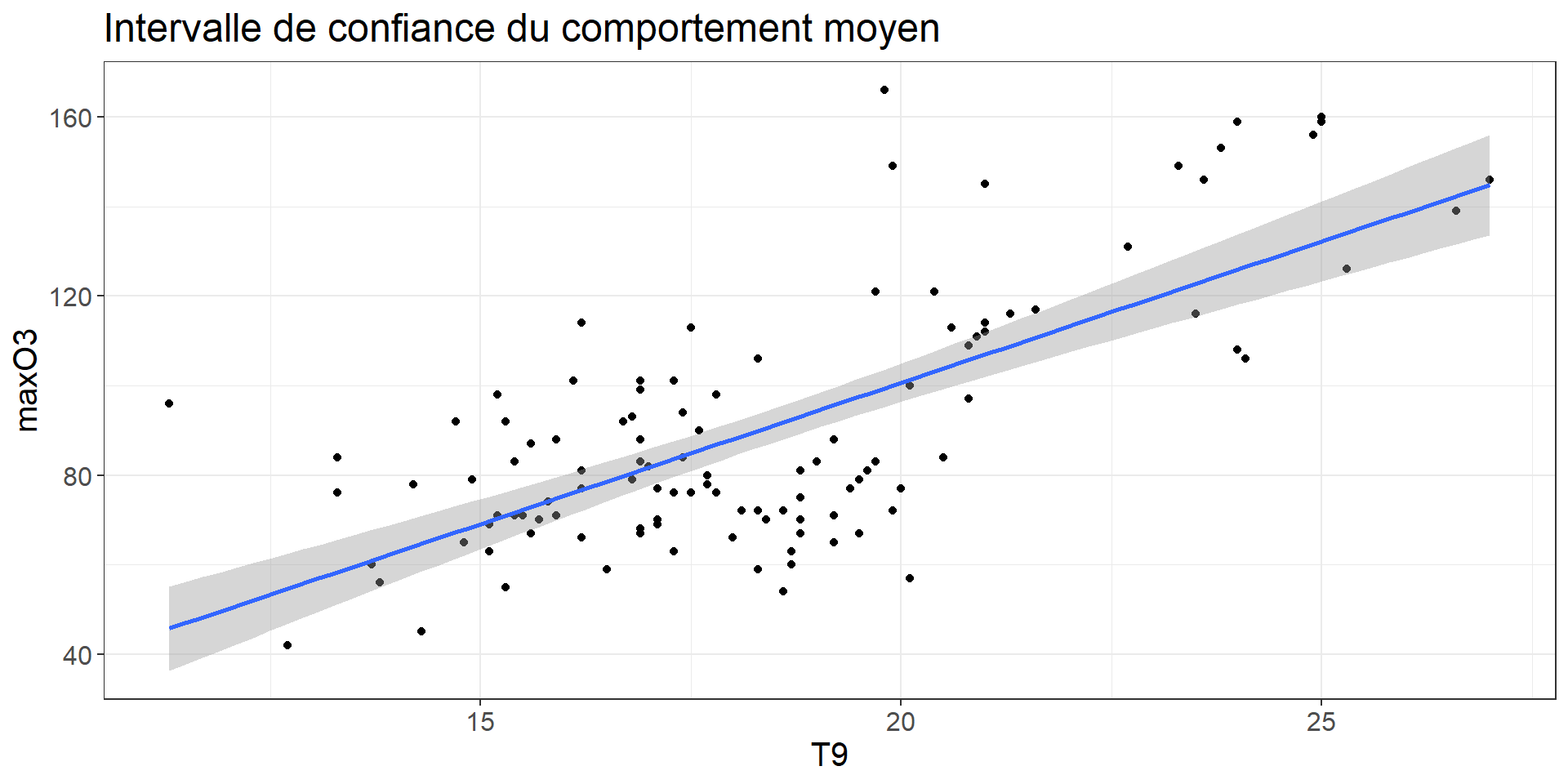
Prédiction et intervalle de confiance
Pour une valeur de x0 particulière, on peut maintenant prédire Y:
ˆY0=ˆβ0+ˆβ1x0
Prédiction de la valeur moyenne de Y pour un x0 particulier
E(ˆY0|x0)∼N(Y0,σ√1n+(x0−ˉx)2∑ni=1(xi−ˉx)2)
Différent de:
Prédiction d’une nouvelle valeur de Y pour un x0 donné (notez le 1 supplémentaire dans la variance).
ˆY0∼N(Y0,σ√1+1n+(x0−ˉx)2∑ni=1(xi−ˉx)2)
Code
data_predict <- bind_cols(data.frame(T9 = ozone$T9), predict(lm(maxO3 ~ T9, data= ozone), interval = "predict"))
ozone %>%
ggplot(aes(x = T9, y = maxO3)) +
geom_point() +
geom_smooth(method ="lm") +# affiche intervalle de confiance par défaut
geom_ribbon(data = data_predict, aes(x = T9, ymax = upr, ymin = lwr, y = fit), alpha = .2, fill = "blue") +
theme_bw()+
labs(title = "Intervalle de confiance du comportement moyen") +
theme(text = element_text(size = 15))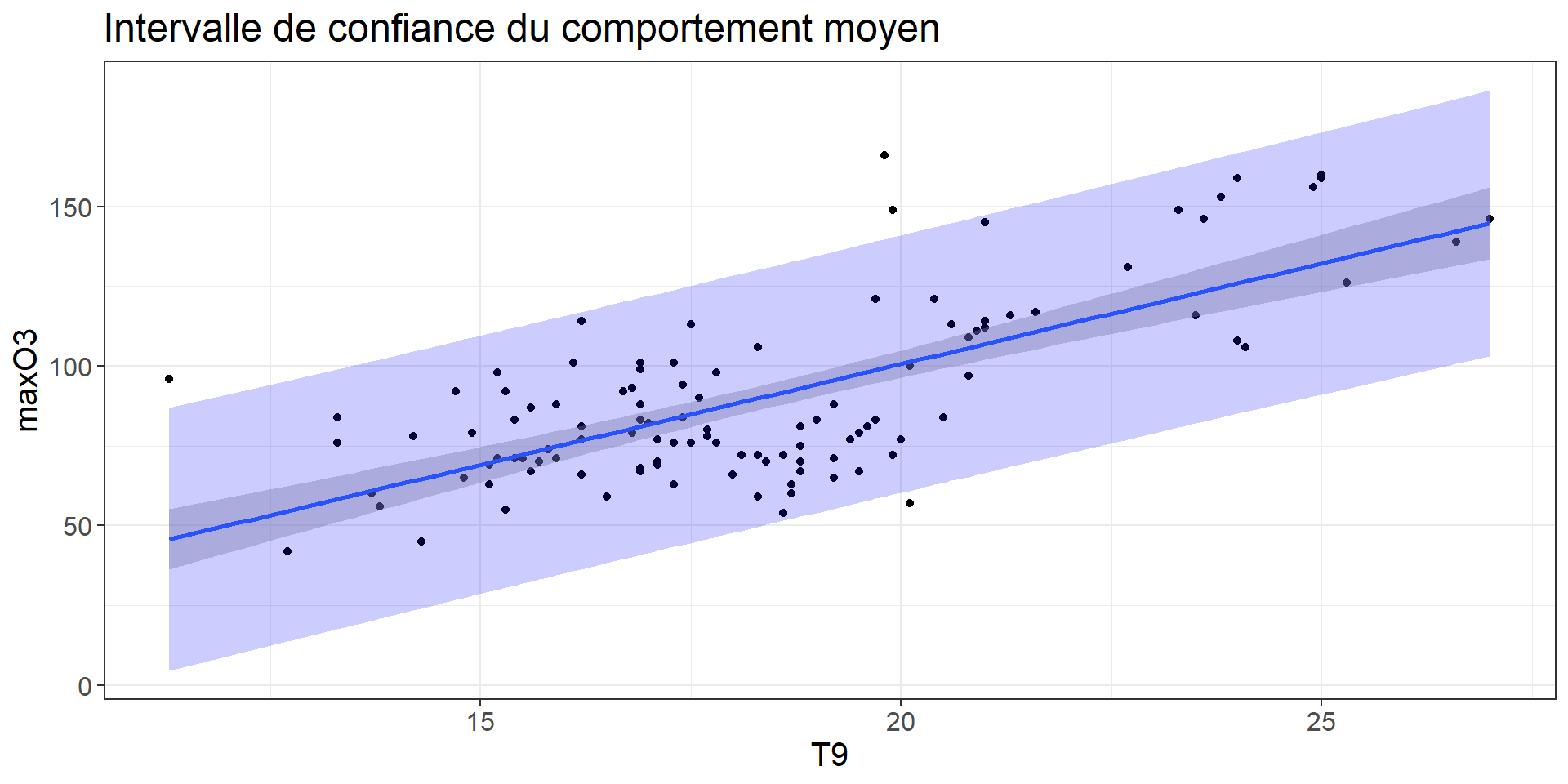
Validité du modèle
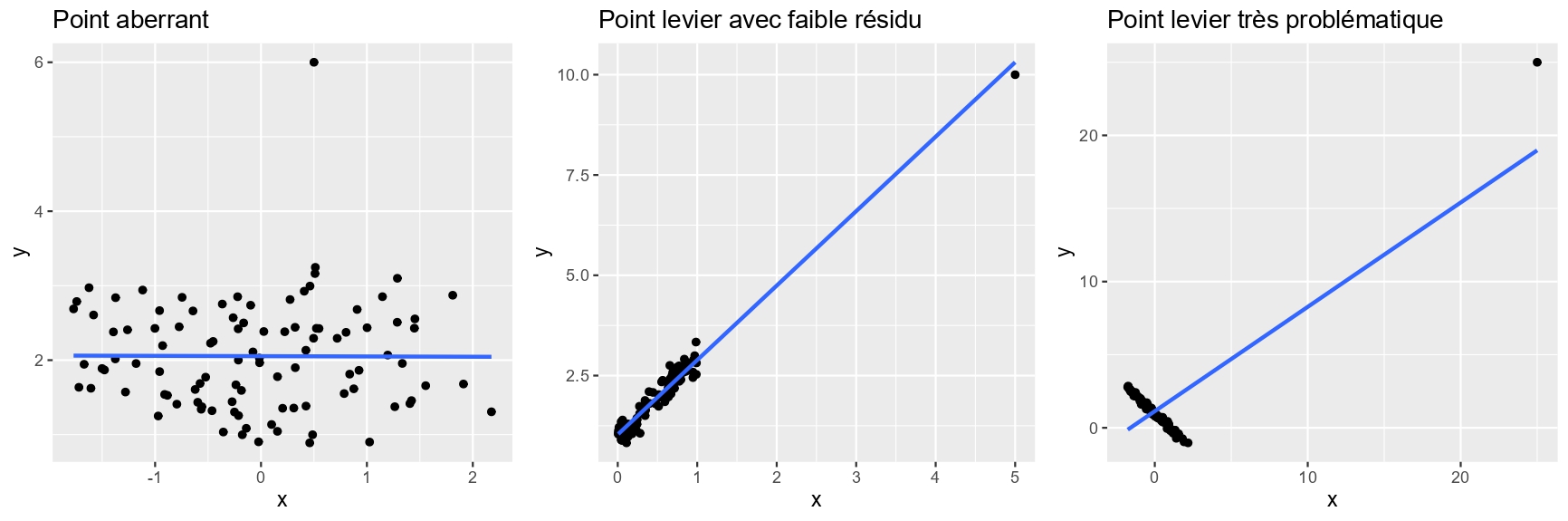
Vérification des hypothèses de départ:
- Normalité des résidus, stabilité de la variance, indépendance des résidus
Construction et sélection de modèle
Modéliser = Comprendre et prévoir
Des exemples de modélisation que vous effectuez tous les jours ?
- Budget pour évènement
- vs
Comment faites-vous ?
- Ex. estimation du budget d’une soirée d’anniversaire
Vous listez les variables ( etc.)
Vous éliminez celles qui sont négligeables (ex. )
Vous quantifiez l’effet des variables restantes
Les statistiques permettent de faire cela avec des phénomènes complexes, en partant de données collectées.
Exemple de problématiques
Prévoir la sévérité d’une maladie fongique en fonction de la météo (P/ETP/T°) et de l’itk (gestion des résidus, sensibilité variétale etc;)
Prédire les potentiels de rendements futurs du soja en France
Potentiel de production éolien en fonction des conditions météorologiques
Objectifs:
Comprendre quelles variables ont une influence sur une variable quanti
Prévoir les valeurs de la variable réponse dans de nouvelles conditions
Régression simple vs multiple
- En régression simple, on ne considérait qu’une seule variable explicative
- En régression multiple, on en considère plusieurs (p)
Réponse=f(var1,var2,...,varp)=var1+var2+...+varp⏟régression linéaire
{∀i=1,...,n εi i.i.d. , E(εi)=0, V(εi)=σ2∀i≠k cov(εi,εk)=0
Une variable quanti peut avoir un effet différent selon différentes modalités d’une quali
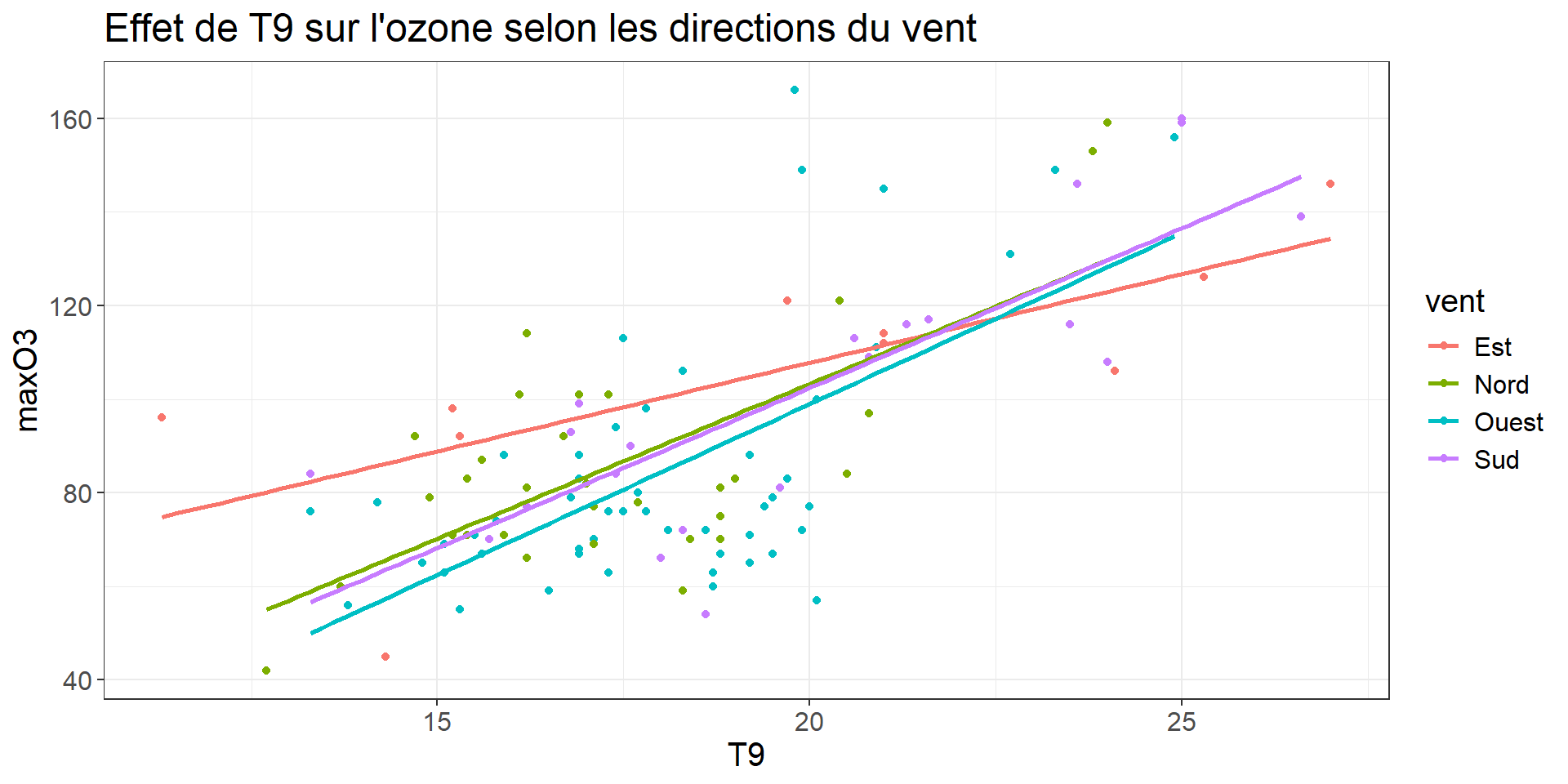
Cela s’écrit ainsi:
MaxO3∼vent+T9+vent:T9
MaxO3ij∼μ+{α1 si vent d'estα2 si vent du nordα3 si vent d'ouestα4 si vent du sud} + (β+{γ1 si vent d'estγ2 si vent du nordγ3 si vent d'ouestγ4 si vent du sud})×T9ij+aleaij {∀i,j Yij=μ+αi+(β+γi)×xij+εij∀i,j εij i.i.d. , E(εij)=0, V(εij)=σ2∀i,j cov(εij,εi′j′)=0
Interaction entre deux variables qualitatives
Définition courante: réaction réciproque de deux phénomènes l’un sur l’autre
Définition statistique : l’effet d’un facteur sur Y diffère selon les modalités de l’autre facteur
library(dplyr)
ozone %>%
group_by(vent, pluie) %>%
summarize(MOY = mean(maxO3)) %>%
ggplot(aes(x=vent, y=MOY, col=pluie, group=pluie)) +
geom_line() +
geom_point() +
labs(title = "Interaction pluie:vent sur maxO3", x = "Direction du vent", y = "Maximum d'ozone") +
theme_bw()+
theme(text = element_text(size = 18))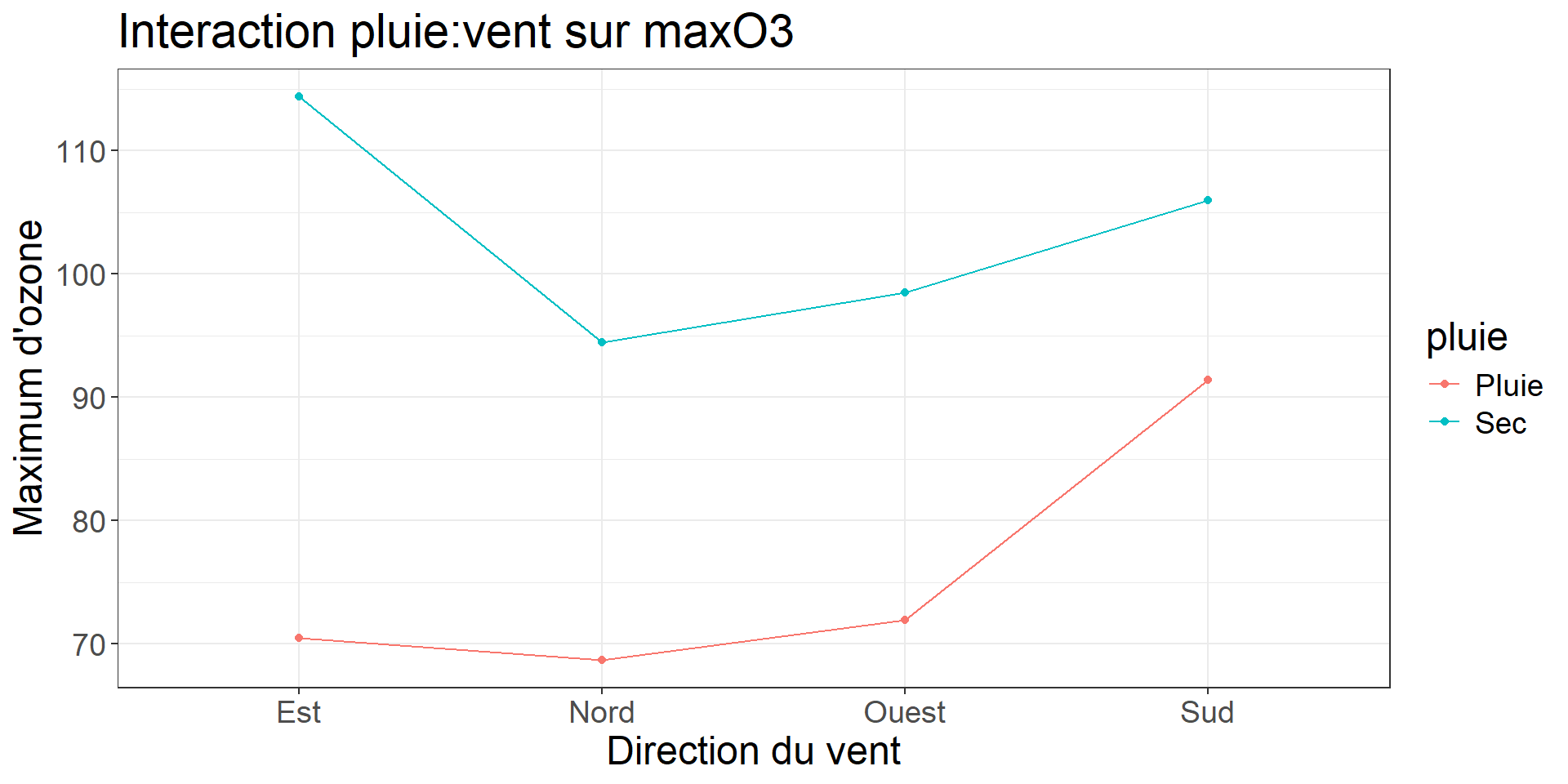
Cela s’écrit ainsi:
MaxO3∼vent+pluie+vent:pluie MaxO3ijk∼μ+{α1 si vent d'estα2 si vent du nordα3 si vent d'ouestα4 si vent du sud}+{β1 si pluieβ2 si sec}+{αβ11 si vent d'est ET pluieαβ12 si vent d'est ET secαβ21 si vent du nord ET pluie⋯αβ42 si vent du sud ET sec}+aleaijk
{∀i,j,k Yijk=μ+αi+βj+αβij+εijk∀i,j,k εijk i.i.d. , E(εijk)=0, V(εijk)=σ2∀i,j,k cov(εijk,εi′j′k′)=0
Quatres types d’effet possibles
Code
theme_set(theme_bw())
ozone %>%
ggplot(aes(x = T9, y = maxO3)) +
geom_point() +
geom_smooth(method ="lm", se= FALSE) +
labs(title = "Quanti sur quanti")+
theme(text = element_text(size = 18))
ozone %>%
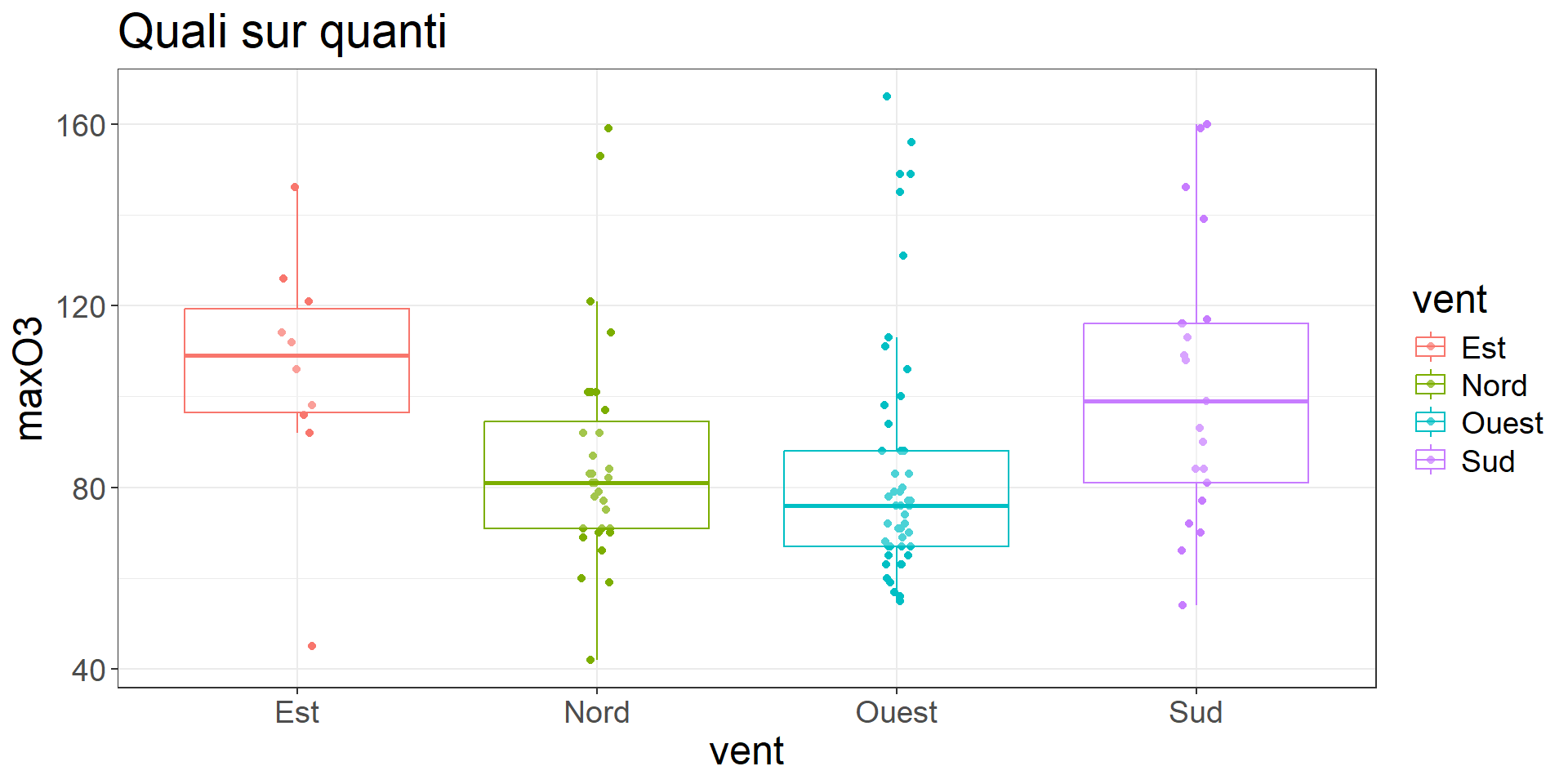
ggplot(aes(x = vent, y = maxO3, color = vent)) +
geom_point(position= position_jitter(width =.05, height= 0)) +
geom_boxplot(alpha= .3, outlier.shape = NA) +
labs(title = "Quali sur quanti") +
theme_bw()+
theme(text = element_text(size = 18))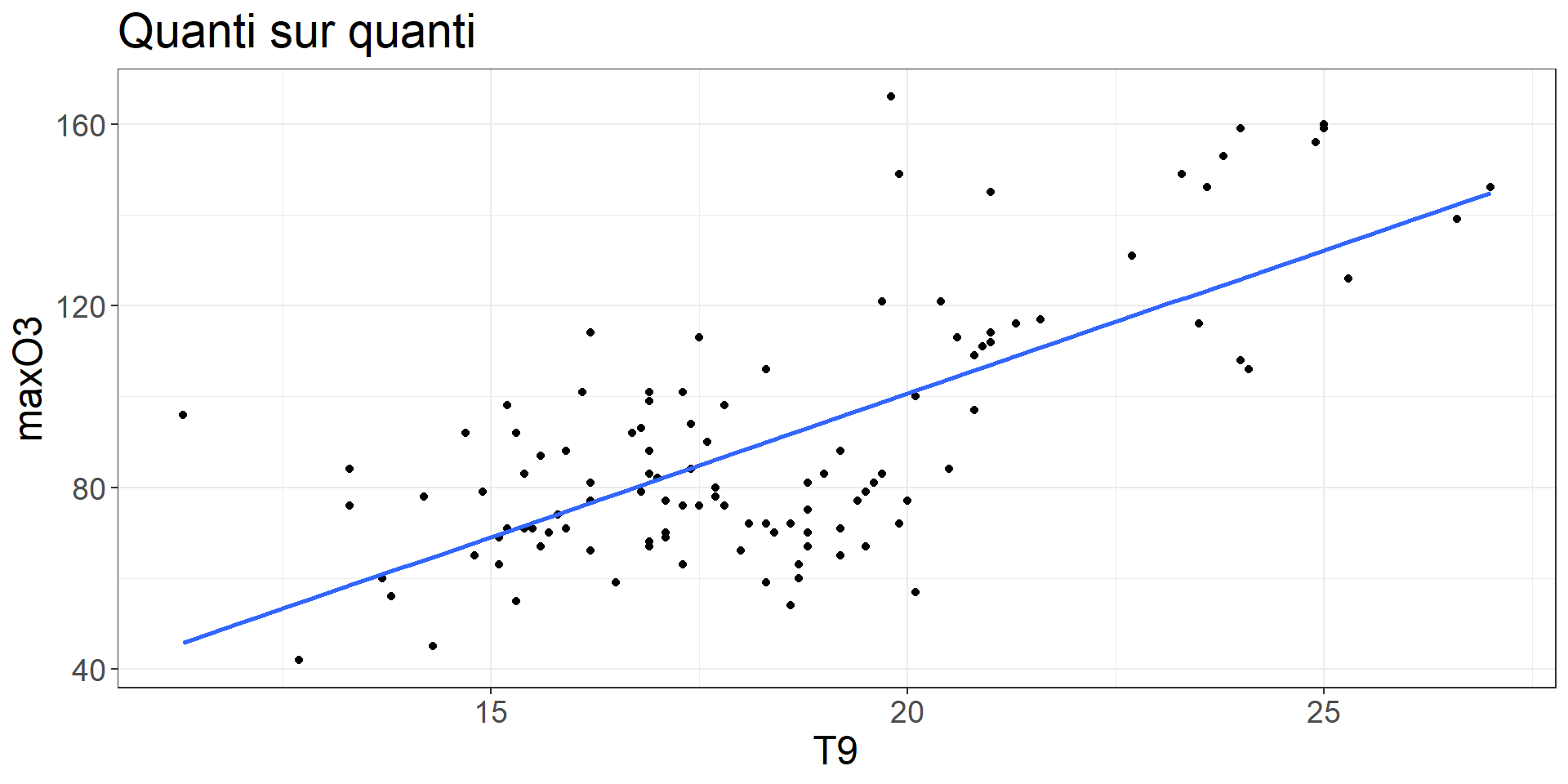
Code
ozone %>%
ggplot(aes(x = T9, y = maxO3, color = vent))+
geom_point() +
geom_smooth(method = "lm", se = FALSE) +
labs(title = "Quali / quanti sur quanti") +
theme_bw()+
theme(text = element_text(size = 18))
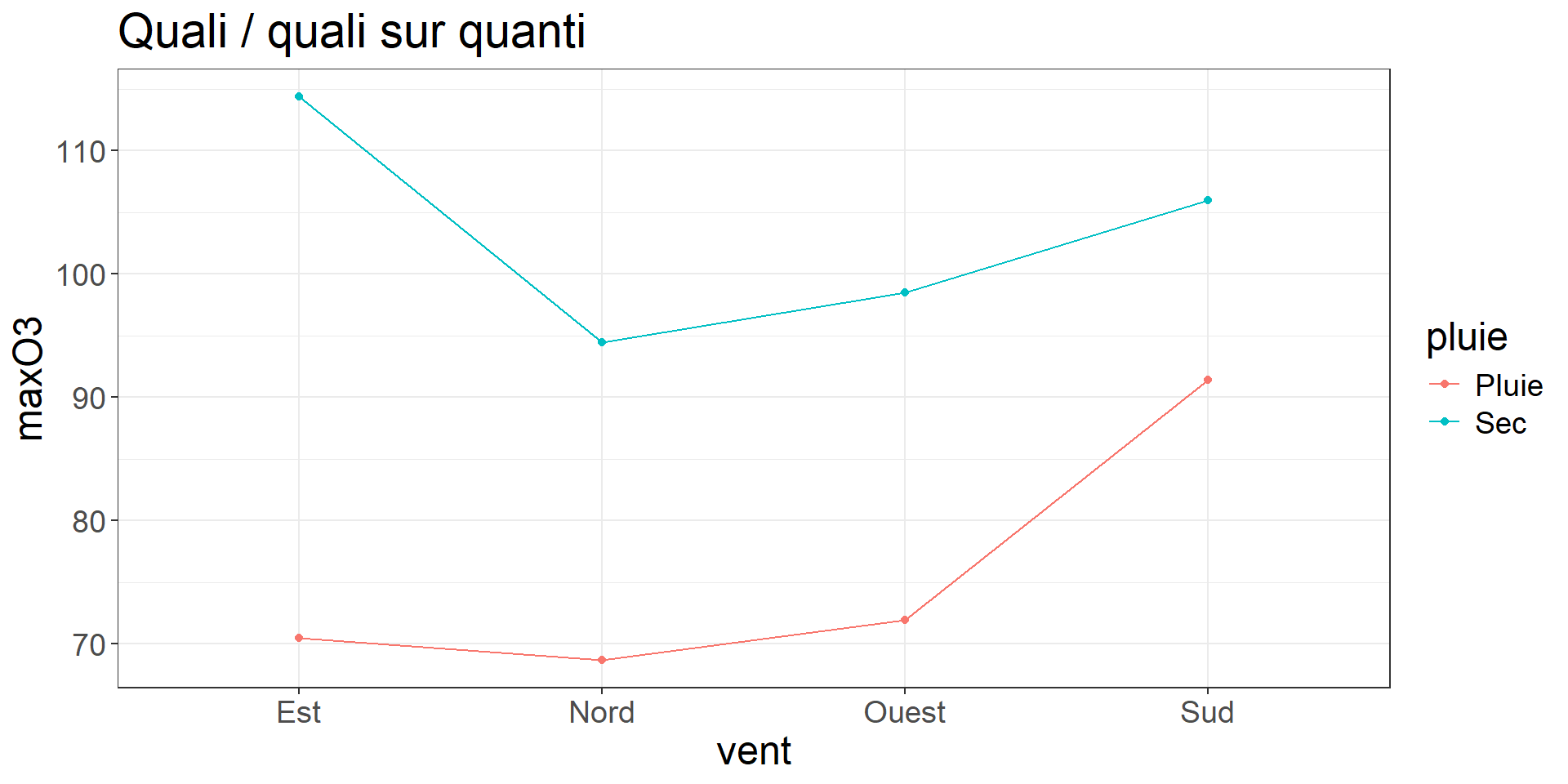
ozone %>%
group_by(vent, pluie) %>%
summarize(MOY = mean(maxO3)) %>%
ggplot(aes(x=vent, y=MOY, col=pluie, group=pluie)) +
geom_line() +
geom_point() +
labs(title = "Quali / quali sur quanti", y = "maxO3") +
theme_bw()+
theme(text = element_text(size = 18))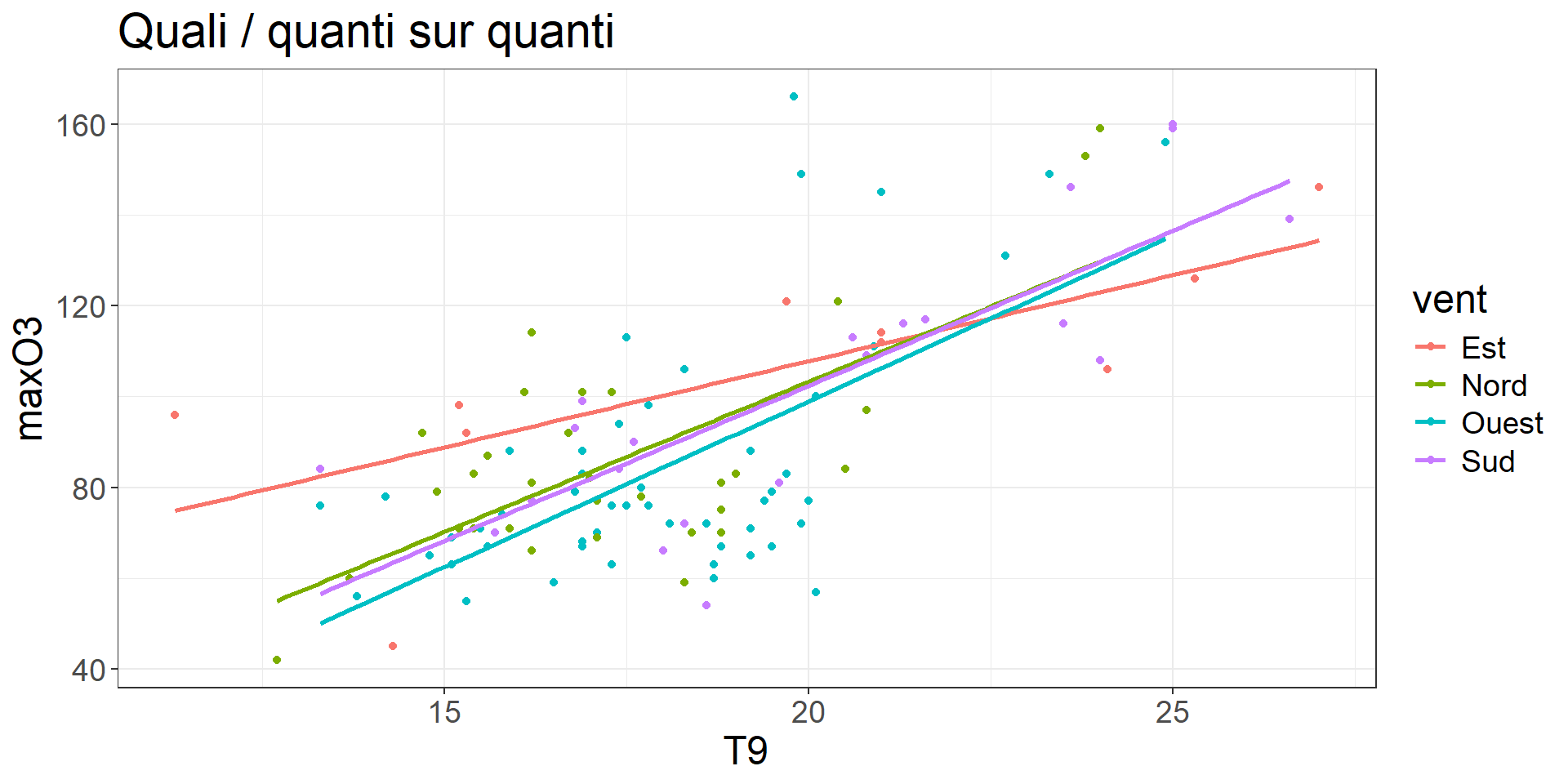
Le(s) modèle(s) linéaire(s)
Le modèle linéaire peut souvent être adapté à des problèmes issu du vivant, modulo quelques points de vigilance
| Réponse | Variable(s) explicative(s) | Méthode |
| Var. quantitative | 1 var. quantitative | régression linéaire simple |
| Var. quantitative | 1 var. qualitative à I modalités | analyse de variance à 1 facteur (rq: si I=2 équivaut à comparaison de 2 moyennes) |
| Var. quantitative | p var. quantitatives | régression linéaire multiple |
| Var. quantitative | K var. qualitatives | analyse de variance à K facteurs |
| Var. quantitative | var. quantitatives et qualitatives | analyse de covariance |
| Var. qualitative (2 catégories) | var. quantitatives et qualitatives | régression logistique |
| Var. qualitative (K catégories) | var. quantitatives et qualitatives | régression multinomiale |
(Re-Re)mettons les mains dans le cambouis
{∀i=1,...,n Yi=β0+β1xi1+β2xi2+β3xi3+...+βpxip+εi∀i=1,...,n εi i.i.d. , E(εi)=0, V(εi)=σ2∀i≠k cov(εi,εk)=0
(p+1) paramètres à estimer + 1 paramètre de variance σ2
Matriciellement : Y=Xβ+E avec E(E)=0, V(E)=σ2Id
(Y1⋮Yi⋮Yn)=β0β1β2…βp(1x11x12⋯x1p⋮⋮⋮1xi1xi2xip⋮⋮⋮⋮1xn1xn2⋯xnp)(β0β1β2⋮βp)+(ε1⋮εi⋮εn)
Rq: ANOVA et ANCOVA peuvent aussi s’écrire sous cette forme.
ANOVA
{∀i,j,k Yijk=μ+αi+βj+αβij+εijk∀i,j,k εijk i.i.d. , E(εijk)=0, V(εijk)=σ2∀i,j,k cov(εijk,εi′j′k′)=0
ANCOVA
{∀i,j Yij=μ+αi+(β+γi)×xij+εij∀i,j εij i.i.d. , E(εij)=0, V(εij)=σ2∀i,j cov(εij,εi′j′)=0
Estimation des paramètres du modèle
Critère des moindres carrés: estimer les paramétres en minimisant la somme des carrés des écarts entre observations et prévisions par le modéle
Y≈Xβ X′Y≈X′Xβ ˆβ=(X′X)−1X′Y si X′X est inversible
Propriétés E(ˆβ)=β; V(ˆβ)=(X′X)−1σ2
La variance des résidus σ2 est estimée par: ˆσ2=∑i(Yi−ˆYi)2nb données−nb paramétres estimés à partir des données E(ˆσ2)=σ2
Décomposition de la variabilité (bis)
| n∑i=1(yi−ˉy)2 | =n∑i=1(ˆyi−ˉy)2 | +n∑i=1(yi−ˆyi)2 | |
| Variabilité | totale | modèle | résiduelle |
Pourcentage de variabilité de Y expliquée par le modèle: R2=SCmodeleSCtotale
Propriétés: R2∈[0,1].
La variabilité du modèle peut être décomposée par variable de 2 façons:
en calculant la variabilité expliquée par chaque variable les unes aprés les autres (pb : la variabilité d’une variable dépend de l’ordre d’introduction des variables)
en calculant la variabilité expliquée exclusivement par une variable (pb : la somme des variabilités de toutes les variables n’est pas égale à la variabilité du modèle)
Dans certains cas (données équilibrées), la variabilité du modéle se décompose parfaitement et ces 2 calculs donnent les mêmes résultats.
Exemple sur ozone
Call:
LinearModel(formula = maxO3 ~ T9 + T12 + T15 + Ne9 + Ne12 + Ne15 +
Vx9 + Vx12 + Vx15 + maxO3v + vent + pluie, data = ozone)
Residual standard error: 14.51 on 97 degrees of freedom
Multiple R-squared: 0.7686
F-statistic: 23.01 on 14 and 97 DF, p-value: 8.744e-25
AIC = 613 BIC = 653.8
Ftest
SS df MS F value Pr(>F)
T9 0.2 1 0.2 0.0011 0.97325
T12 376.0 1 376.0 1.7868 0.18445
T15 30.3 1 30.3 0.1439 0.70526
Ne9 1016.5 1 1016.5 4.8312 0.03033
Ne12 37.9 1 37.9 0.1803 0.67208
Ne15 0.1 1 0.1 0.0003 0.98680
Vx9 50.2 1 50.2 0.2388 0.62619
Vx12 35.7 1 35.7 0.1697 0.68127
Vx15 122.6 1 122.6 0.5826 0.44715
maxO3v 5560.4 1 5560.4 26.4261 1.421e-06
vent 297.8 3 99.3 0.4718 0.70267
pluie 182.9 1 182.9 0.8694 0.35344
Residuals 20410.2 97 210.4
Ttest
Estimate Std. Error t value Pr(>|t|)
(Intercept) 20.762962 15.461879 1.3428 0.18245
T9 0.039170 1.164957 0.0336 0.97325
T12 1.972574 1.475705 1.3367 0.18445
T15 0.450308 1.187073 0.3793 0.70526
Ne9 -2.109755 0.959855 -2.1980 0.03033
Ne12 -0.605592 1.426338 -0.4246 0.67208
Ne15 -0.017178 1.035894 -0.0166 0.98680
Vx9 0.482609 0.987624 0.4887 0.62619
Vx12 0.513795 1.247167 0.4120 0.68127
Vx15 0.726623 0.951976 0.7633 0.44715
maxO3v 0.344378 0.066991 5.1406 1.421e-06
vent - Est -2.874041 5.157999 -0.5572 0.57867
vent - Nord -2.334477 2.890844 -0.8075 0.42133
vent - Ouest 2.662276 3.658288 0.7277 0.46853
vent - Sud 2.546243 3.061435 0.8317 0.40761
pluie - Pluie -1.623565 1.741257 -0.9324 0.35344
pluie - Sec 1.623565 1.741257 0.9324 0.35344Test de l’effet d’une ou plusieurs variables
L’ensemble de variables V apporte-t-il des informations complémentaires intéressantes sachant que les autres variables sont déjé dans le modèle ?
Hypothèses : H0:“tous les coefficients associés aux variables de V sont égaux à 0” contre H1 : “au moins un coefficient des variables V≠ 0
Statistique de test: Fobs=SCV/ddlVSCR/ddlR=CMVCMR
Loi de la statistique de test: Sous H0, L(Fobs)=FddlVddlR
Décision : P(FddlRddlV>Fobs)<0.05 ⟹ Rejet de H0
Revient à choisir entre le sous-modèle sans les variables V ou le modèle complet
Si V contient tous les effets : revient à tester si R2 est significativement différent de 0, i.e. si toutes les variables sont inutiles (versus au moins une utile)
On somme les degrés de liberté associés é l’ensemble V sachant qu’1 variable quanti à 1 ddl, 1 variable quali à I−1 ddl et une interaction a comme ddl le produit des ddl de chaque facteur
Sélection de variables
Sélection de modèle = trouver un compromis entre un modèle qui s’ajuste bien aux données et qui n’a pas “trop” de paramètres (Rappel: )
- Souvent utilisé: sélection du modèle qui minimise l’AIC / BIC: compromis entre maximisation de la vraisemblance L (à quel point le modèle s’ajuste bien aux données) et le nb de paramètres
AIC=2p−2ln(ˆL)
BIC=pln(n)−2ln(ˆL)
A votre avis, quelle est la différence entre les 2 critères ( !)
Plusieurs stratégies
- Construction exhaustive de tous les sous-modèles (long et même impossible si trop de variables)
- Méthode descendante (backward): construire le modéle complet; supprimer la variable explicative la moins intéressante et reconstruire le modèle sans cette variable; itérer jusqu’à ce que toutes les variables explicatives soient intéressantes
- Méthode ascendante (forward): partir du modéle avec la variable la plus intéressante; ajouter la variable qui, connaissant les autres variables du modèle, apporte le plus d’information complémentaire; itérer jusqu’é ce qu’aucune variable n’apporte d’information intéressante
- Méthode stepwise: compromis entre les 2 méthodes ci-dessus
Exemple sur ozone: sélection de variables
Results for the complete model:
==============================
Call:
LinearModel(formula = maxO3 ~ ., data = ozone, selection = "bic")
Residual standard error: 14.51 on 97 degrees of freedom
Multiple R-squared: 0.7686
F-statistic: 23.01 on 14 and 97 DF, p-value: 8.744e-25
AIC = 613 BIC = 653.8
Results for the model selected by BIC criterion:
===============================================
Call:
LinearModel(formula = maxO3 ~ T12 + Ne9 + Vx9 + maxO3v, data = ozone,
selection = "bic")
Residual standard error: 14 on 107 degrees of freedom
Multiple R-squared: 0.7622
F-statistic: 85.75 on 4 and 107 DF, p-value: 1.763e-32
AIC = 596 BIC = 609.6
Ftest
SS df MS F value Pr(>F)
T12 6650.4 1 6650.4 33.9334 6.073e-08
Ne9 2714.8 1 2714.8 13.8522 0.0003172
Vx9 903.4 1 903.4 4.6094 0.0340547
maxO3v 7363.5 1 7363.5 37.5721 1.499e-08
Residuals 20970.2 107 196.0
Ttest
Estimate Std. Error t value Pr(>|t|)
(Intercept) 12.631310 11.000877 1.1482 0.2534427
T12 2.764090 0.474502 5.8252 6.073e-08
Ne9 -2.515402 0.675845 -3.7219 0.0003172
Vx9 1.292857 0.602180 2.1470 0.0340547
maxO3v 0.354832 0.057888 6.1296 1.499e-08Démarche en modélisation
Lister les variables potentiellement explicatives / prédictives
Visualiser
Selectionner le sous-modèle (minimisation de l’AIC ou du BIC)
Interpréter les résultats (quelles variables ressortent ? Est-ce surprenant ? Est-ce en accord avec les connaissances sur le sujet ? Des confusions possibles ?)
Interpréter les coefficients (signe, valeur etc.)
(Prédire pour de nouvelles valeurs)
Codage et contraintes pour variables quali
La matrice de design X (dans Y=Xβ+E) a autant de lignes que d’individus. Pour les colonnes, c’est variable…
| Constante (μ ou β0) | Variable quanti | Variable Quali | Interaction quali -quali | |
|---|---|---|---|---|
| Représentation dans X | Une colonne de 1 | Valeur de la variable | (I-1) colonnes par modalités de chaque variable à I modalités | (I-1)*(J-1) colonnes |
| Degrés de libertés (ddl) | 1 | 1 | I-1 | (I-1)*(J-1) |
| Commentaires | Contrainte à poser sur les paramètres (le mieux est ∑Ii=1αi=0) | Contrainte à poser sur les paramètres (le mieux est ∀i,∑jαβij=0 et ∀j,∑iαβij=0) |
Important
Le choix de la contrainte impacte FORTEMENT l’interprétation
- ∑iαi=0, la comparaison est faite par rapport à la moyenne des moyennes par modalité
- α1=0, la comparaison est faite par rapport à un niveau de ref (moins intuitif, et pas pratique quand présence d’interactions)
Certaines fonctions de R par défaut utilisent la contrainte 2. !
Comparez les sorties de ces différentes lignes de code…
Inteprétation des résultats
- Modèle sélectionné ⇒ Interprétation des résultats
2 situations
- Idéale: données équilibrées
- Difficile: données déséquilibrées
Remarques:
- Les plans d’expériences permettent d’avoir données équilibrées
- En ANOVA, on a souvent des données équilibrées
Décomposition de la variabilité : variables quali, données équilibrées
Quand les données sont équilibrées, la décomposition de la variabilité est parfaite:
∑i,j,k(yijk−y∙∙∙)2=∑i,j,k(yi∙∙−y∙∙∙)2⏟ˆα2i+∑i,j,k(y∙j∙−y∙∙∙)2⏟ˆβ2j+∑i,j,k(yij∙−yi∙∙−y∙j∙+y∙∙∙)2⏟^αβ2ij+∑i,j,k(yijk−yij∙)2⏟ε2ijk
Quand les données sont équilibrées, les coefficients s’estiment simplement:
ˆμ=y∙∙∙ ∀i, ˆαi=yi∙∙−y∙∙∙∀j, ˆβj=y∙j∙−y∙∙∙ ∀i,j ^αβij=yij∙−yi∙∙−y∙j∙+y∙∙∙
⟹ On quantifie parfaitement ce qui est expliqué par chaque variable ou interaction
Comparaison de moyennes ajustées
Moyennes ajustées = ˆμ+ˆαi: Permet de s’affranchir de l’effet des autres variables
Comparaisons possibles 2 à 2, moyennant une correction de Bonferroni par ex.
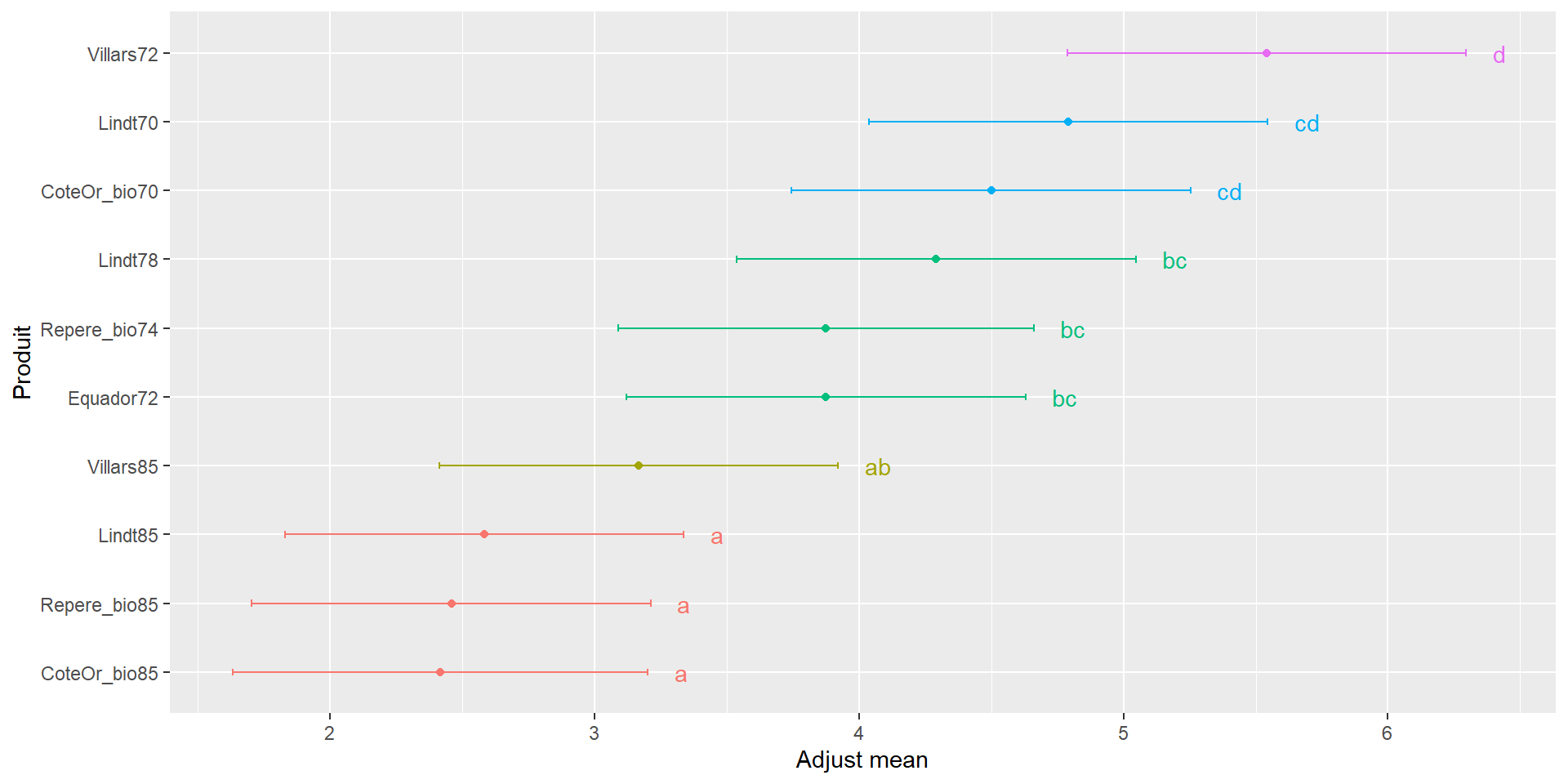
$adjMean
Produit emmean SE df lower.CL upper.CL
CoteOr_bio70 4.50 0.264 118 3.75 5.25
CoteOr_bio85 2.42 0.275 118 1.63 3.20
Equador72 3.88 0.264 118 3.12 4.63
Lindt70 4.79 0.264 118 4.04 5.55
Lindt78 4.29 0.264 118 3.54 5.05
Lindt85 2.58 0.264 118 1.83 3.34
Repere_bio74 3.88 0.275 118 3.09 4.66
Repere_bio85 2.46 0.264 118 1.70 3.21
Villars72 5.54 0.264 118 4.79 6.30
Villars85 3.17 0.264 118 2.41 3.92
Results are averaged over the levels of: Juge
Confidence level used: 0.95
Conf-level adjustment: bonferroni method for 10 estimates
$groupComp
CoteOr_bio85 Repere_bio85 Lindt85 Villars85 Equador72 Repere_bio74
"a" "a" "a" "ab" "bc" "bc"
Lindt78 CoteOr_bio70 Lindt70 Villars72
"bc" "cd" "cd" "d"
attr(,"class")
[1] "meansComp"Prédictions
ˆY=^β0+^β1xi1+^β2xi2+...+^βpxip
Prédire Y pour : (T12=19, Ne9=8, Vx9=1.2, maxO3v=70) et (T12=23, Ne9=10, Vx9=0.9, maxO3v=95)
Sur PC:
fit lwr upr
1 71.41544 42.90026 99.93063
2 85.92393 56.76803 115.07983 fit lwr upr
1 71.41544 64.86327 77.96761
2 85.92393 76.98627 94.86159Analyse des résidus
Les résidus sont la part du phénomène non-expliquée par le modèle
On peut vérifier les hypothèses initiales du modèle
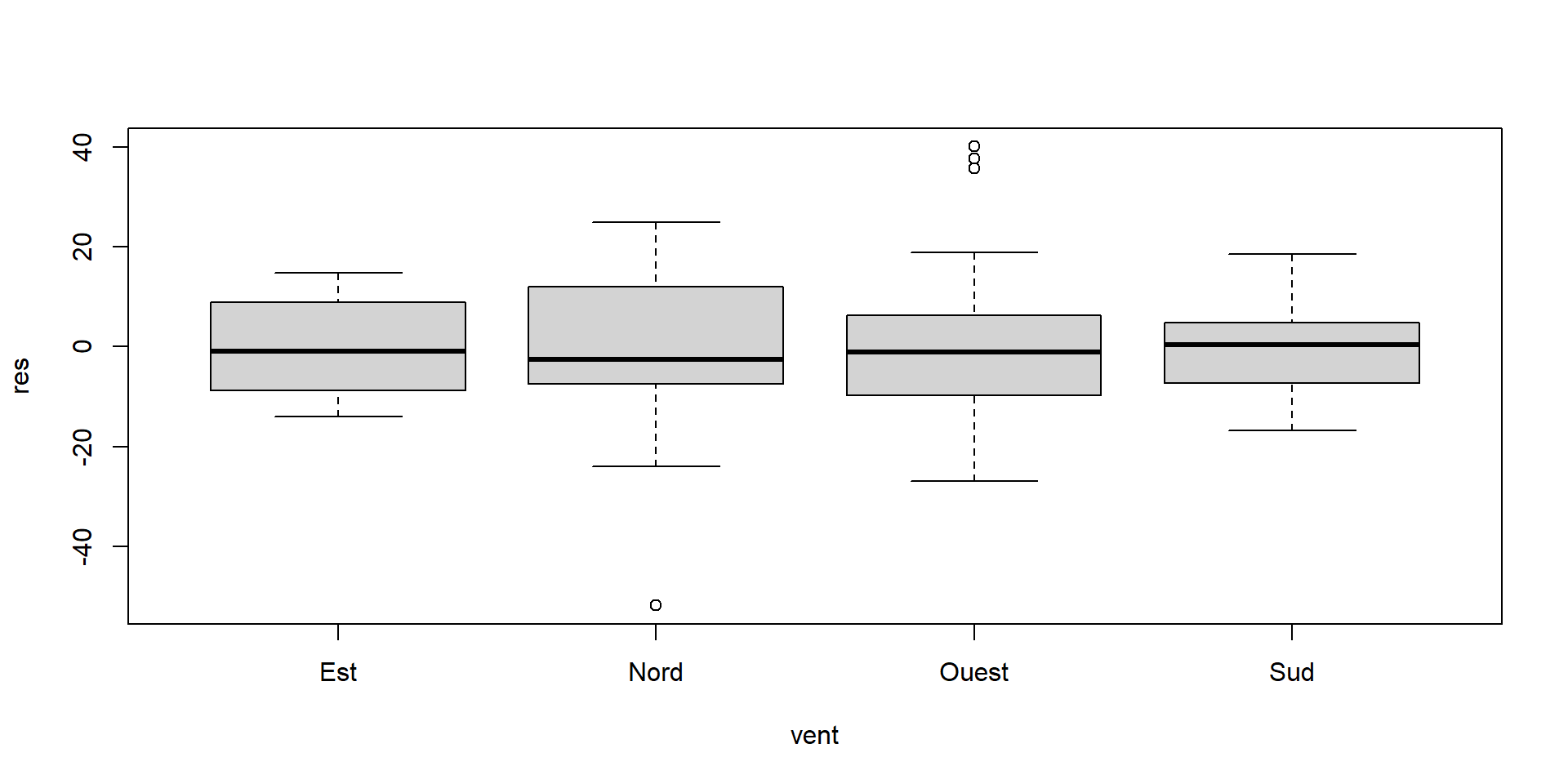
Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 3 1.5589 0.2036
108 - Test de Shapiro-Wilk de normalité des Résidus (Rq : la non-normalité n’est pas un pb tant que la distribution est symétrique)
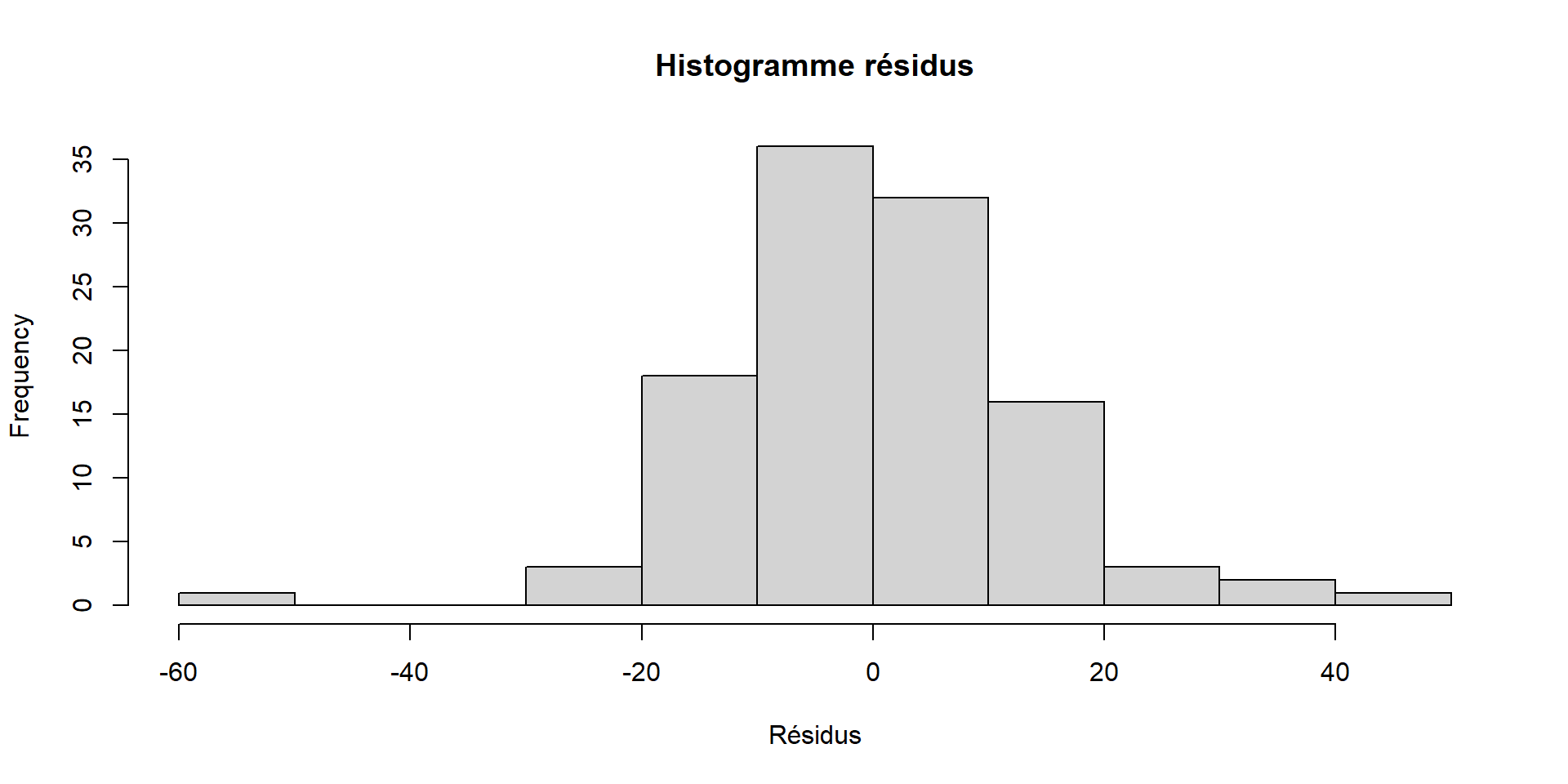
Shapiro-Wilk normality test
data: res
W = 0.97117, p-value = 0.01587Retour sur l’exemple ozone
- Maximum d’ozone : variable réponse
- Les variables de températures, nébulosité, vitesse de vent (quanti), et la direction et la pluie (quali) sont prises en compte
- On ne sait pas si les interactions entre variables quali et entre les variables quali et quanti sont négligeables ⟹ on les met dans le modèle
LinearModel(maxO3 ~ (T9 + T12 + T15 + Ne9 + Ne12 + Ne15 + Vx9 + Vx12 + Vx15 + maxO3v + pluie + vent) * (pluie + vent), data=ozone, selection="bic")
Ce qui revient à écrire :
maxO3 ~ T9 + T12 + T15 + Ne9 + Ne12 + Ne15 + Vx9 + Vx12 + Vx15 + maxO3v + pluie + vent + T9:pluie + T12:pluie + T15:pluie + Ne9:pluie + Ne12:pluie + Ne15:pluie + Vx9:pluie + Vx12:pluie + Vx15:pluie + maxO3v:pluie + vent:pluie + T9:vent + T12:vent + T15:vent + Ne9:vent + Ne12:vent + Ne15:vent + Vx9:vent + Vx12:vent + Vx15:vent + maxO3v:vent
Résultat et sortie
Results for the complete model:
Call: LinearModel(formula = maxO3 ~ (T9 + T12 + T15 + Ne9 + Ne12 + Ne15 + Vx9 + Vx12 + Vx15 + maxO3v + pluie + vent) * (pluie + vent), data = ozone, selection = "bic")
Residual standard error: 14.54 on 56 degrees of freedom Multiple R-squared: 0.8658 F-statistic: 6.569 on 55 and 56 DF, p-value: 2.585e-11 AIC = 634 BIC = 786.2
Results for the model selected by BIC criterion:
Call: LinearModel(formula = maxO3 ~ T9 + T15 + Ne12 + Vx9 + maxO3v + vent + T9:vent + T15:vent, data = ozone, selection = "bic")
Residual standard error: 13.8 on 97 degrees of freedom Multiple R-squared: 0.7906 F-statistic: 26.16 on 14 and 97 DF, p-value: 8.082e-27 AIC = 601.8 BIC = 642.6
Interprétation des résultats
SS df MS F value Pr(>F)
T9 606.2 1 606.2 3.1841 0.0775 .
T15 252.8 1 252.8 1.3278 0.2520
Ne12 2107.0 1 2107.0 11.0664 0.0012 **
Vx9 1657.3 1 1657.3 8.7046 0.0040 **
maxO3v 5160.8 1 5160.8 27.1060 <2e-16 ***
vent 12.5 3 4.2 0.0218 0.9956
T9:vent 2587.1 3 862.4 4.5294 0.0051 **
T15:vent 3722.1 3 1240.7 6.5165 0.0005 ***
Residuals 18468.3 97 190.4
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1On peut dire (à partir des effets significatifs) qu’il y a, sur le max d’O3:
- des effets de nébulosité de vitesse de vent, du maximum d’O3 de la veille
- des effets de la direction du vent et des températures mais à travers les interactions : la direction du vent modifie l’effet de la To (i.e. amplifie l’effet de la To ou la diminue selon la direction du vent) sur max O3
On peut aussi dire (à partir des absences d’effets significatifs):
- la pluviométrie n’est pas un facteur déterminant qui influe sur le max d’03
- une seule nébulosité (Ne12) est conservée dans le modèle : cela ne veut pas dire que les autres nébulosités n’ont pas d’effet (elles peuvent avoir un effet similaire). Idem pour la vitesse de vent.
- pour la To, on a besoin des To à 9h et à 15h pour mieux prévoir le maximum d’ozone. L’effet de la To n’est pas exactement le même entre 9h et 15h (mais 12h n’est pas utile comme info)
- l’effet de la nébulosité est le même quelle que soit la direction du vent. Idem pour la vitesse du vent.
Interprétation des résultats (2/2)
Estimate Std. Error t value Pr(>|t|)
(Intercept) 18.2063 13.7059 1.3284 0.1872
T9 1.8269 1.0238 1.7844 0.0775
T15 1.0200 0.8852 1.1523 0.2520
Ne12 -3.0132 0.9058 -3.3266 0.0012
Vx9 2.2213 0.7529 2.9504 0.0040
maxO3v 0.3467 0.0666 5.2063 0.0000
vent - Est 0.4734 17.0102 0.0278 0.9779
vent - Nord 3.2974 15.0356 0.2193 0.8269
vent - Ouest -1.1250 14.0066 -0.0803 0.9361
vent - Sud -2.6458 15.1489 -0.1747 0.8617
vent - Est : T9 -4.7442 2.1418 -2.2151 0.0291
vent - Nord : T9 6.1408 1.7014 3.6093 0.0005
vent - Ouest : T9 -0.9505 1.3455 -0.7064 0.4816
vent - Sud : T9 -0.4460 1.5222 -0.2930 0.7701
vent - Est : T15 3.6810 1.7967 2.0487 0.0432
vent - Nord : T15 -5.2279 1.2153 -4.3016 0.0000
vent - Ouest : T15 0.9797 0.9308 1.0525 0.2952
vent - Sud : T15 0.5673 1.1111 0.5105 0.6108- pour T9 et T15, β ≠ 0
- nébulosité, max d’O3 ( )
- maximum d’O3 de la veille est grand, maximum d’O3 du jour
- les jours de vents d’est et surtout du nord ont des max d’O3 supérieur aux jours de vents d’ouest et du sud
- les jours de vent du nord, l’effet de la To à 9h est plus important (coef =6.14); au contraire quand le vent vient de l’est. C’est l’inverse pour la To à 15h
- Ainsi, quand le vent du nord, l’effet de la To à 9h est particulièrement fort (donc s’il fait chaud à 9h quand le vent vient du nord, le max d’O3 risque d’être important)
- etc.
Démarche en modélisation (bis)
Lister les variables potentiellement explicatives / prédictives
Visualiser
Selectionner le sous-modèle (minimisation de l’AIC ou du BIC)
Interpréter les résultats (quelles variables ressortent ? Est-ce surprenant ? Est-ce en accord avec les connaissances sur le sujet ? Des confusions possibles ?
Interpréter les coefficients (signe, valeur etc.)
Prédire pour de nouvelles valeurs
Annexes
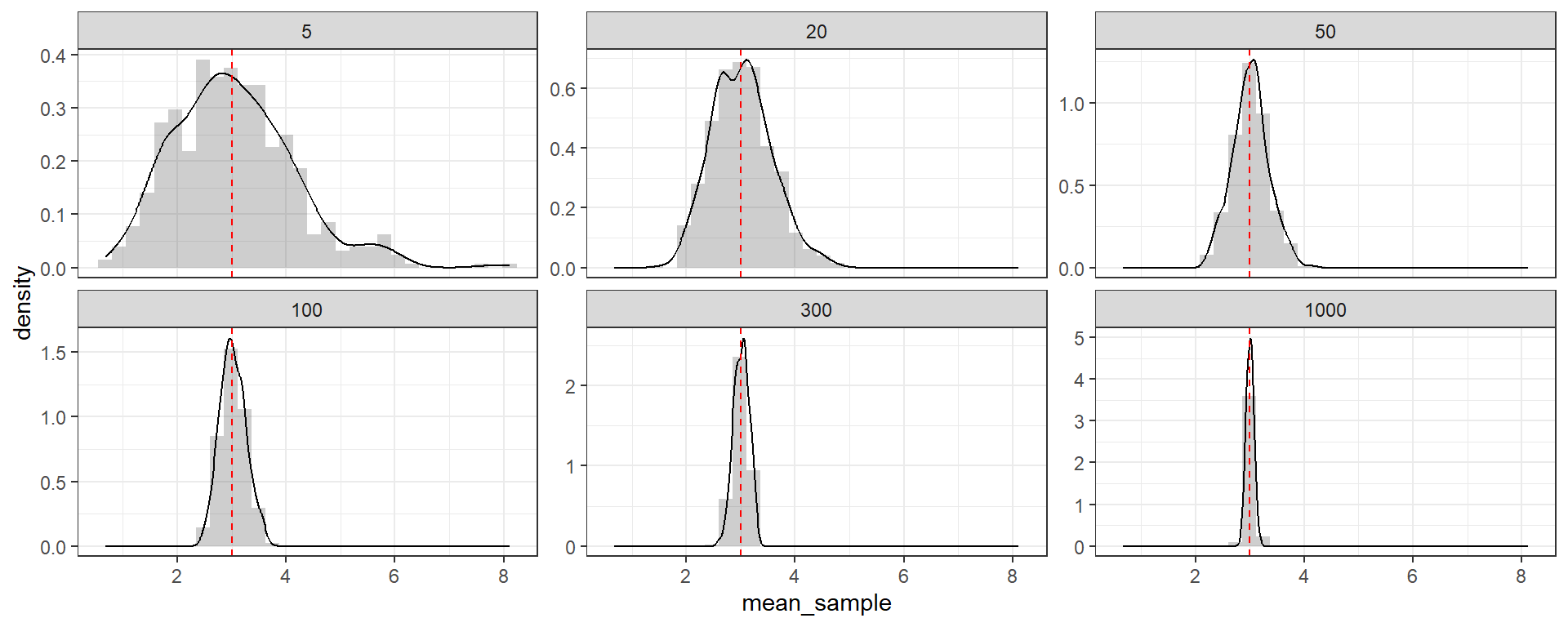
Le TCL, c’est PUISSANT
- Ce que dit le TCL, c’est que peu importe la distribution de base, les moyennes empiriques d’échantillons issues cette distribution auront une distribution normale centrée sur l’espérance de la distribution !
Une simulation rapide pour visualiser les choses
- Ex distribution χ2(3)
- On connaît la vraie moyenne de cette loi: 3
Mais dans la vraie vie, on aurait accès qu’à un échantillon de cette loi, par ex. de taille n=50. Regardons comment évolue la distribution des moyennes empiriques en fonction de la taille de l’échantillon.